In wireless communications and other applications of digital signal processing, we often want to modify a generated or acquired signal. A device or algorithm that performs some prescribed operations on an input signal to generate an output signal is called a system. Amplifiers in communication receivers and filters in image processing applications are some systems that we interact with in daily lives. Our main focus in these articles will be on a particular class of systems which are linear and time-invariant.
A linear system implies that if two inputs are scaled and summed together to form a new input, the new output of the system is also a scaled sum of their individual outputs.
[Scaling] For scaling to hold, if
\begin{align*}
\text{input} \quad s_1[n] ~& \xrightarrow~ r_1[n] \quad \text{output}
\end{align*}
then
\begin{align*}
\text{input}\quad \alpha s_1[n] ~& \xrightarrow~ \alpha r_1[n] \quad \text{output}
\end{align*}
where $\alpha$ is any scalar.
[Addition] When two such inputs are added together, the output should be the sum of their individual outputs as
\begin{align*}
\text{input}\quad s_1[n] + s_2[n] ~& \xrightarrow~ r_1[n] + r_2[n] \quad \text{output}
\end{align*}
A linear system combines the above two properties as
\begin{align}\label{eqIntroductionLinearity}
\text{input}\quad \alpha_1 s_1[n] + \alpha_2 s_2[n] ~& \xrightarrow~ \alpha_1 r_1[n] + \alpha_2 r_2[n] \quad \text{output}
\end{align}
Below, we discuss examples of a linear and a non-linear system.
Consider a system
\begin{equation*}
r[n] = \frac{3}{7} \cdot s[n]
\end{equation*}
The output of this system, as a response to an input $s_1[n] = \sin(2\pi 0.1n)$, is
\begin{equation*}
r_1[n] = \frac{3}{7}\sin(2\pi 0.1n)
\end{equation*}
Similarly, response to a different signal $s_2[n] = \sin(2\pi 0.3n)$ is
\begin{equation*}
r_2[n] = \frac{3}{7}\sin(2\pi 0.3n)
\end{equation*}
When this system is given the input $s_1[n] + s_2[n]$, the output is
\begin{align*}
r[n] &= \frac{3}{7}\left\{\sin(2\pi 0.1n) + \sin(2\pi 0.3n)\right\} \\
&= \frac{3}{7}\sin(2\pi 0.1n) + \frac{3}{7}\sin(2\pi 0.3n) \\
&= r_1[n] + r_2[n]
\end{align*}
Hence, it is a linear system.
On the other hand, when the same input $s_1[n] + s_2[n]$ is given to another system
\begin{equation*}
r[n] = s^2[n]
\end{equation*}
and using the identity $\sin(A)\sin(B) = \frac{1}{2}\{\cos(A-B) – \cos(A+B)\}$, the output is
\begin{align*}
r[n] &= \left\{\sin(2\pi 0.1n) + \sin(2\pi 0.3n) \right\}^2 \\
&= \sin^2(2\pi 0.1n) + \sin^2(2\pi 0.3n) + 2\sin(2\pi 0.1 n) \sin(2\pi 0.3 n) \\
&= \sin^2(2\pi 0.1n) + \sin^2(2\pi 0.3n) + \cos(2\pi 0.2n) – \cos(2\pi 0.4n) \\
& \neq r_1[n] + r_2[n] \\
&= \sin^2(2\pi 0.1n) + \sin^2(2\pi 0.3n)
\end{align*}
Clearly, it is a non-linear system.
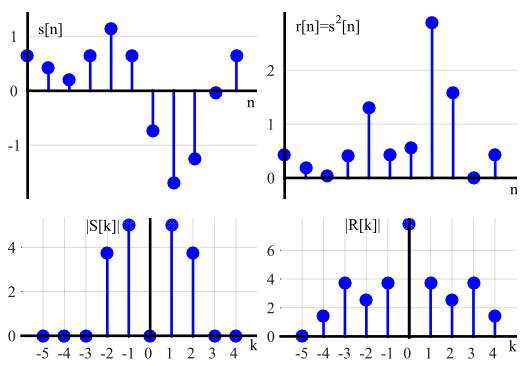
From above example, it is also clear that input sinusoids do not interact with each other in linear systems, and hence output frequencies were the same as the input frequencies. In a non-linear system, however, input sinusoids interacted with each other to produce frequencies that were not present in either of the input signal, as shown in Figure below for $r[n] = s^2[n]$. Note from $|S[k]|$ that $s(t)$ actually consists of only two frequencies at bins $1$ and $2$, but the output $[r[n]$ of the system is composed of other frequencies as well shown in $|R[k]|$.
The Discrete Fourier Transform, DFT, is a linear operation as it is evident from its definition that any scaling and addition of two or more input signals will result in a DFT output that is a scaled and summed version of their individual DFT outputs.
Wherever you are reading these lines, have a look around and you will find that most of the things with straight lines are made by humans such as books, tables and buildings. And most of the natural stuff is non-linear or curved such as plants, mountains and meteors. This is not only an indication of the difference between nature and us but also that human designs work reasonably well.