Linear Time-Invariant (LTI) Archives | Page 2 of 2

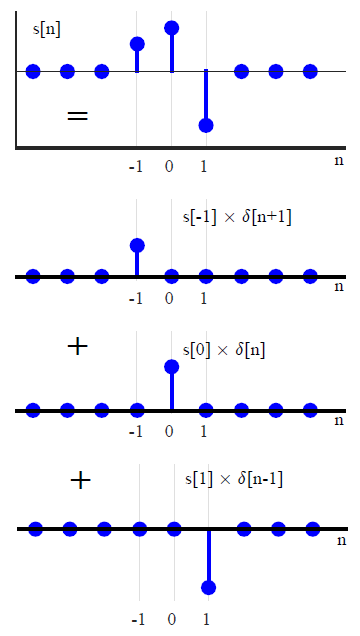
A signal broken down into scaled and shifted impulses

August 9, 2016 DSP

Convolution

Understanding convolution is the biggest test DSP learners face. After knowing about what a system is, its types and its impulse response, one wonders if there is any method through which an output signal of a system can be determined for a given input signal. Convolution is the answer to that question, provided that the system is linear and time-invariant (LTI). We start with real signals and LTI systems with real impulse responses. The case of complex signals and systems will be discussed later. Convolution of Real Signals Assume that we have an arbitrary signal $s[n]$. Then, $s[n]$ can be

July 30, 2016 DSP

Correlation

Correlation is a foundation over which the whole structure of digital communications is built. In fact, correlation is the heart of a digital communication system, not only for data detection but for parameter estimation of various kinds as well. Throughout, we will find recurring reminders of this fact. As a start, consider from the article on Discrete Fourier Transform that each DFT output $S[k]$ is just a sum of term-by-term products between an input signal and a cosine/sine wave, which is actually a computation of correlation. Later, we will learn that to detect the transmitted bits at the receiver, correlation

July 29, 2016 DSP

Linear Systems

In wireless communications and other applications of digital signal processing, we often want to modify a generated or acquired signal. A device or algorithm that performs some prescribed operations on an input signal to generate an output signal is called a system. Amplifiers in communication receivers and filters in image processing applications are some systems that we interact with in daily lives. Our main focus in these articles will be on a particular class of systems which are linear and time-invariant. A linear system implies that if two inputs are scaled and summed together to form a new input, the

July 21, 2016 DSP

Some DFT Properties

The purpose of this article is to summarize some useful DFT properties in a table. My favorite property is the beautiful symmetry depicted by continuous and discrete Fourier transforms. However, if you feel that this particular content is not as descriptive as the other posts on this website are, you are right. As opposed to the rest of the content on the website, we do not intend to derive all the properties here. Instead, based on what we have learned, some important properties of the DFT are summarized in the table below with an expectation that the reader can derive

July 20, 2016 DSP

Time-Invariant Systems

A system is time-invariant if shifting the input sequence on time axis leads to an equivalent shift of the output sequence along the time axis, with no other changes.