Tag: Phase Shift Keying (PSK)

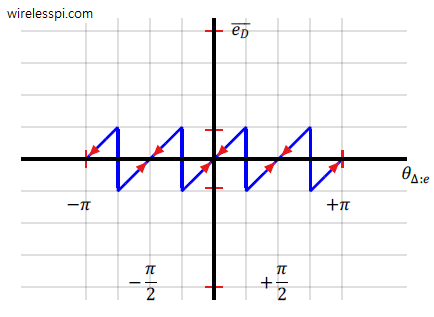
Multiple stable lock points in the S-curve of a decision-directed loop
Wireless/SDR

Resolving Phase Ambiguity through Unique Word and Differential Encoding and Decoding

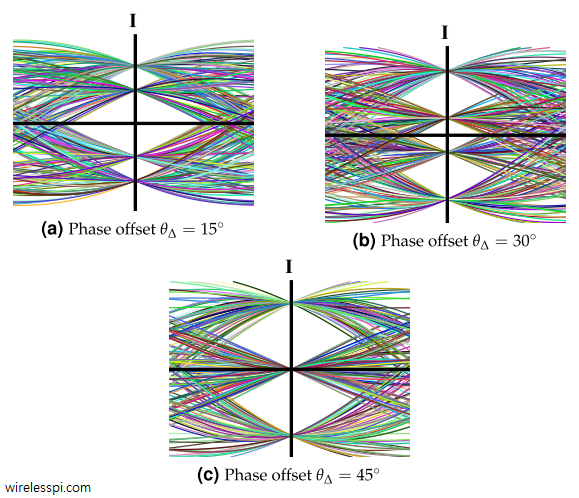
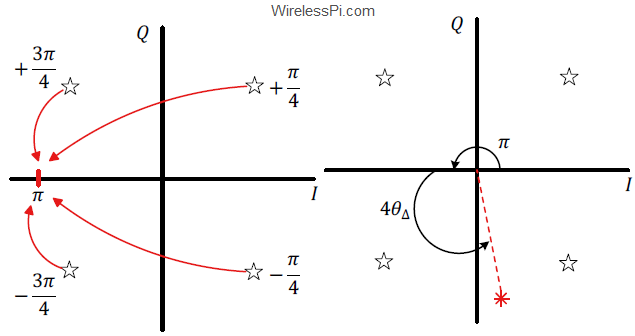
In the context of carrier synchronization, we have discussed the Costas loop and other techniques before. Today, we discuss the significance of differential encoding and decoding for phase ambiguity resolution. Keep in mind that this topic is different than differential detection. In the former case, the data bits are encoded before modulation and decoded after demodulation in a differential manner. Nevertheless, the demodulation is still coherent (i.e., it requires carrier synchronization). In the latter case, the data symbols are detected during demodulation through differential operations, thus canceling the effect of channel phase and eliminating the need for carrier synchronization. Let

Continue reading
Eye diagrams for I arm of a 4-QAM signal for 15, 30 and 45 degrees phase offsets and a Raised Cosine filter with excess bandwidth 0.5. A similar eye diagram exists for Q arm as well
Wireless/SDR

What is Carrier Phase Offset and How It Affects the Symbol Detection

In case of Quadrature Amplitude Modulation (QAM) and other passband modulation schemes, Rx has no information about carrier phase of the Tx oscillator. Let us explore what impact this has on the demodulation process. Constellation Rotation To see the effect of the carrier phase offset, consider that a transmitted passband signal consists of two PAM waveforms in $I$ and $Q$ arms denoted by $v_I(t)$ and $v_Q(t)$ respectively and combined as \begin{equation}\label{eqRealWorldQAMPhaseOffset} s(t) = v_I(t) \sqrt{2} \cos 2\pi F_C t – v_Q(t) \sqrt{2}\sin 2\pi F_C t \end{equation} Here, $F_C$ is the carrier frequency and $v_I(t)$ and $v_Q(t)$ are the continuous versions

Continue reading
An illustration of wiping off the modulation process without any training information
Wireless/SDR

Non-Data-Aided Carrier Phase Estimation

A carrier phase offset rotates the Rx constellation causing decision errors even in a perfectly noiseless environment. One of the techniques used to overcome this problem is to insert a known sequence at the start of the transmission known as a preamble. Then, the Rx can utilize these known symbols in the arriving signal to estimate the carrier phase and de-rotate the constellation. However, inserting a known sequence within the message decreases the spectral efficiency of the system. To avoid this cost, a phase estimator (as well as estimators for other distortions) can be derived in a non-data-aided fashion. One

Continue reading