Quadrature Phase Shift Keying (QPSK) Archives

March 23, 2025 DSP / Wireless/SDR

Two Birds with One Tone: I/Q Signals and Fourier Transform – Part 1

When a new member arrives at the DSP club, this is what they find at the club gate: I/Q signals. Perhaps a secret plot to keep most people out of the party? Some return from here to try another area (e.g., machine learning, which pays more and is easier to understand but less interesting than DSP). Others persist enough to push the gate open (even a little understanding is sufficient for this task). So what exactly makes this topic so mysterious? To investigate the answer, we start with an example audio signal drawn in the figure below that displays amplitude

Eye diagram for a 4-QAM modulated signal and a simple channel impulse response

December 30, 2016 Wireless/SDR

Impact of Multipath on the Received Signal

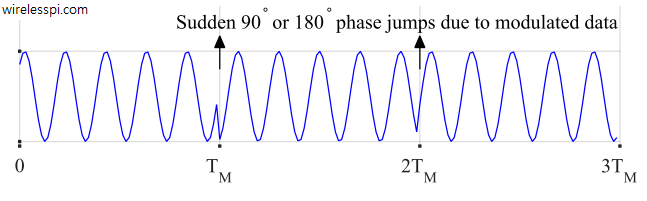
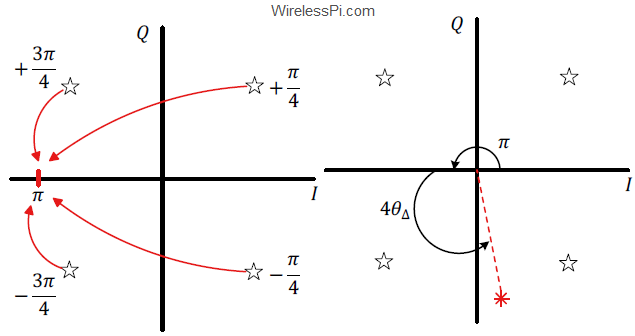
In this article, we describe the impact of multipath caused by the wireless channel on the signal arriving at the receiver from a constellation viewpoint. Recall that an eye diagram, a transition diagram and a scatter plot are the stethoscopes of a communication system and hence it is imperative to bring in that perspective for a Tx signal convolved with the channel impulse response. This is because a wireless channel can be seen as a Finite Impulse Response (FIR) filter with the result that the sampled Rx signal is a convolution between taps of this FIR filter and the Tx

Phase jumps at every zero crossing from modulating data onto the carrier phase for a QPSK waveform

October 7, 2016 Wireless/SDR

The Fundamental Problem of Synchronization

We have seen in the effect of phase rotation that the matched filter outputs do not map back perfectly onto the expected constellation, even in the absence of noise and no other distortion. Unless this rotation is small enough, it causes the symbol-spaced optimal samples to cross the decision boundary and fall in the wrong decision zone. And even for small rotations, relatively less amount of noise can cause decision errors in this case, i.e., noise margin is reduced. In fact, for higher-order modulation, the rotation becomes even worse because the signals are closely spaced with each other for the

A general QAM detector with respective waveforms at each block

October 7, 2016 Wireless/SDR

Quadrature Amplitude Modulation (QAM)

Quadrature Amplitude Modulation (QAM) is a spectrally efficient modulation scheme used in most of the high-speed wireless networks today. We discussed earlier that Pulse Amplitude Modulation (PAM) transmits information through amplitude scaling of the pulse $p(nT_S)$ according to the symbol value. To understand QAM, two routes need to be traversed. Route 1 We start the first route with differentiating between baseband and passband signals. A baseband signal has a spectral magnitude that is nonzero only for frequencies around origin ($F=0$) and negligible elsewhere. An example spectral plot for a PAM waveform is shown below for 500 2-PAM symbols shaped by

MSK as a special case of both non-linear and linear modulation schemes

January 25, 2017 Wireless/SDR

Minimum Shift Keying (MSK) – A Tutorial

Minimum Shift Keying (MSK) is one of the most spectrally efficient modulation schemes available. Due to its constant envelope, it is resilient to non-linear distortion and was therefore chosen as the modulation technique for the GSM cell phone standard. MSK is a special case of Continuous-Phase Frequency Shift Keying (CPFSK) which is a special case of a general class of modulation schemes known as Continuous-Phase Modulation (CPM). It is worth noting that CPM (and hence CPFSK) is a non-linear modulation and hence by extension MSK is a non-linear modulation as well. Nevertheless, it can also be cast as a linear