Aliasing Archives | Page 2 of 2

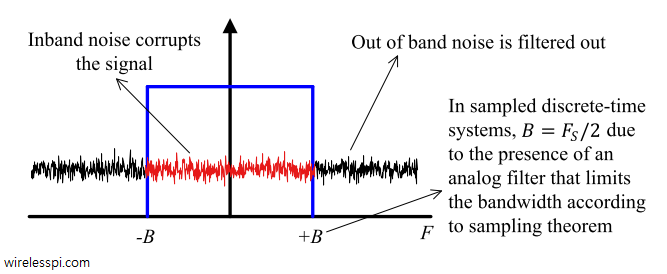
Computing noise power within a specified bandwidth

August 15, 2016 Wireless/SDR

Additive White Gaussian Noise (AWGN)

The performance of a digital communication system is quantified by the probability of bit detection errors in the presence of thermal noise. In the context of wireless communications, the main source of thermal noise is addition of random signals arising from the vibration of atoms in the receiver electronics. You can also watch the video below. The term additive white Gaussian noise (AWGN) originates due to the following reasons: [Additive] The noise is additive, i.e., the received signal is equal to the transmitted signal plus noise. This gives the most widely used equality in communication systems. \begin{equation}\label{eqIntroductionAWGNadditive} r(t) = s(t)

A rectangular signal and its upsampled version in time and frequency domains

August 3, 2016 DSP

Sample Rate Conversion

In the discussion on sampling, the process of sampling a continuous-time signal was discussed in detail and subsequently sampling theorem was derived. In many applications, resampling an already digitized signal is mandatory for an efficient system design. In wireless communications, sample rate conversion is utilized for upconversion and downconversion to a desired frequency, filtering stages in the digital frontend and sometimes for carrier and timing synchronization during signal acquisition. See the Cascade Integrator Comb (CIC) filters for how to accomplish this task with minimal resources. In discrete domain, sample rate can be reduced by discarding intermediate samples periodically called downsampling

A prism decomposes the white light into 7 colours

August 2, 2016 DSP

The Discrete Fourier Transform (DFT)

Learned in some other articles on this website, the following three important concepts take us to the core of the Discrete Fourier Transform (DFT) idea. Regardless of the signal shape, most signals of practical interest can be considered as a sum of complex sinusoids oscillating at different frequencies. A set of $N$ orthogonal complex sinusoids can be constructed within a span of $N$ time domain samples. Each `tick’ or bin on the discrete frequency axis denotes the discrete frequency $k/N$ of such a complex sinusoid. To understand how a set of sinusoids with $N$ discrete frequencies can sum up to

July 17, 2016 DSP

Sampling a Continuous-Time Signal

Most signals of our interest — wireless communication waveforms — are continuous-time as they have to travel through a real wireless channel. To process such a signal using digital signal processing techniques, the signal must be converted into a sequence of numbers. This can be done through the process of periodic sampling. From Continuous to Discrete Time Consider a band-limited continuous-time signal $s(t)$ and its frequency domain representation $S(F)$ with bandwidth $B$, shown in the above figure. A discrete-time signal $s[n]$ can be obtained by taking samples of $s(t)$ at equal intervals of $T_S$ seconds. This process is shown in

Illustration of peak ISI and asymmetry about -3dB point

July 18, 2016 DSP / Wireless/SDR

Pulse Shaping Filter

In digital logic, a stream of 1s and 0s forms a sequence of rectangular pulses, which can be easily identified at the receiver side by a threshold. In time domain, everything looks nice and perfect. Let us investigate the system characteristics in frequency domain. In a Pulse Amplitude Modulation (PAM) system, the main component that defines the spectral contents of the signal is the pulse shape $p(nT_S)$ at the Tx. We start with our attention towards a simple rectangular pulse shape. Here is a brief outline of what we cover in this article. Table of Contents 1. Spectrum of a