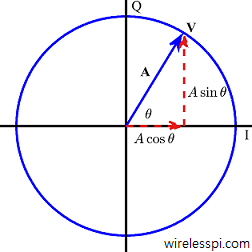
Although complex notation is not complex to understand, I attempt to avoid complex notation altogether while writing DSP articles. If you are interested in where these complex numbers come from, you can read my real-imaginative guide to complex numbers. A complex number is defined as an ordered pair of real numbers in $(x,y)$-plane. In that respect, complex numbers can be considered as vectors with initial point on the origin $(0,0)$. Addition of complex numbers is then similar to the addition of vectors in $(x,y)$-plane from this perspective. However, multiplication is well defined for complex numbers while it is not defined
Continue reading