Dealing with Complex Numbers

Although complex notation is not complex to understand, I attempt to avoid complex notation altogether while writing DSP articles. If you are interested in where these complex numbers come from, you can read my real-imaginative guide to complex numbers.

A complex number is defined as an ordered pair of real numbers in $(x,y)$-plane. In that respect, complex numbers can be considered as vectors with initial point on the origin $(0,0)$. Addition of complex numbers is then similar to the addition of vectors in $(x,y)$-plane from this perspective.

However, multiplication is well defined for complex numbers while it is not defined for vectors — the dot product of two vectors is a scalar, not a vector, while the cross product of two vectors in a plane is a vector that is outside of that plane. The product of complex numbers, on the other hand, is a complex number — an extremely useful property.

For our purpose, using the complex numbers but still staying clear of the complex notation means that we focus on a 2-dimensional plane with $x$ or real-axis named as $I$ (which stands for inphase) and $y$ or imaginary-axis named as $Q$ (which stands for quadrature). In the post about frequency, we will learn why the $x$ and $y$ components are called inphase and quadrature, respectively.

Magnitude and Phase

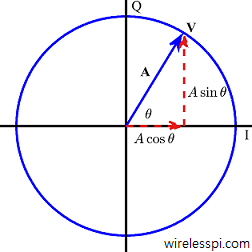
In polar representation of complex numbers, the magnitude of $V$ in an $IQ$-plane is defined as

Defining the phase $\measuredangle V$ is a little trickier. It is tempting to define it as $\tan^{-1} V_Q/V_I$. However, a problem with this is that
\begin{align*}
\tan^{-1} \frac{+V_Q}{+V_I} ~&=~ \tan^{-1} \frac{-V_Q}{-V_I} \quad \rightarrow \quad \text{in}~ [0,+\pi/2],~ \text{quadrant I} \\
\tan^{-1} \frac{-V_Q}{+V_I} ~&=~ \tan^{-1} \frac{+V_Q}{-V_I} \quad \rightarrow \quad \text{in}~ [0,-\pi/2],~ \text{quadrant IV}
\end{align*}

There is no way to differentiate whether $V$ lies in quadrant I or III. The same holds for $V$ lying in quadrant II or IV. In practice, $V$ can lie in any quadrant and its phase should be in the range $[-\pi,\pi)$ because

• Quadrant I: $\measuredangle V$ should be in $[0,\pi/2]$
• Quadrant II: $\measuredangle V$ should be in $[\pi/2,\pi]$
• Quadrant III: $\measuredangle V$ should be in $[-\pi/2,-\pi]$
• Quadrant IV: $\measuredangle V$ should be in $[0,-\pi/2]$

Similarly, from the figure below,

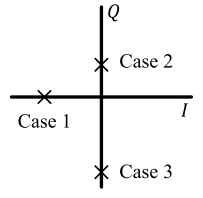
• Case 1: When $V_I<0$ and $V_Q=0$, the phase of $V$ should be $\pi$, not $0$
• Case 2: When $V_I=0$ and $V_Q>0$, the phase of $V$ should be $+\pi/2$
• Case 3: When $V_I=0$ and $V_Q<0$, the phase of $V$ should be $-\pi/2$

Taking into account all four quadrants, $\measuredangle V$ is defined in terms of $\tan^{-1} (V_Q/V_I)$ as

This adjustment is usually known as four-quadrant inverse tangent which can be computed in hardware using efficient techniques..

Addition and Multiplication Operations

The addition and multiplication rules for complex numbers are explained below.

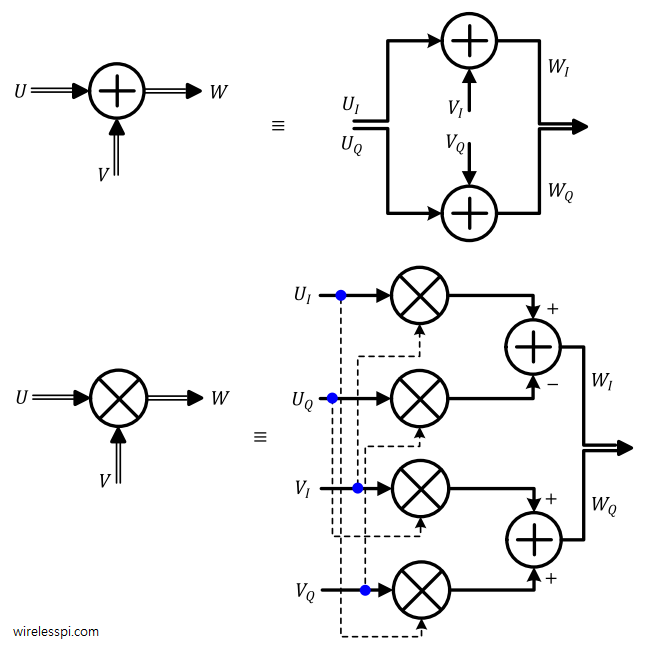
Addition rule above makes perfect sense: both $I$ components are added together as well as both $Q$ components. The multiplication rule seems a little strange though: $I$ is a difference between products of two aligned-axes terms (i.e., $I\cdot I$ – $Q\cdot Q$), while $Q$ is a sum of products of two cross-axes terms (i.e., $Q\cdot I$ + $I\cdot Q$).

To see why multiplication of two complex numbers is perfectly logical, consider that $U_I = |U| \cos \measuredangle U$ and $U_Q = |U| \sin \measuredangle U$, while $V_I = |V| \cos \measuredangle V$ and $V_Q = |V| \sin \measuredangle V$. Therefore,
\begin{align*}
W_I\: &= |U| \cos \measuredangle U \cdot |V| \cos \measuredangle V – |U| \sin \measuredangle U \cdot |V| \sin \measuredangle V \\
W_Q &= |U| \sin \measuredangle U \cdot |V| \cos \measuredangle V + |U| \cos \measuredangle U \cdot |V| \sin \measuredangle V
\end{align*}
which leads to
\begin{align*}
W_I\: &= |U| |V| \left(\cos \measuredangle U \cdot \cos \measuredangle V – \sin \measuredangle U \cdot \sin \measuredangle V \right) \\
W_Q &= |U| |V| \left( \sin \measuredangle U \cdot \cos \measuredangle V + \cos \measuredangle U \cdot \sin \measuredangle V \right)
\end{align*}

Using the identities $\cos A \cos B – \sin A \sin B = \cos (A+B)$ and $\sin A$ $\cos B$ $+$ $\cos A \sin B = \sin (A+B)$,
\begin{align*}
W_I\: &= |U| |V| \cos \left(\measuredangle U + \measuredangle V \right) \\
W_Q &= |U| |V| \sin \left( \measuredangle U + \measuredangle V \right)
\end{align*}
Hence, multiplication of two complex numbers is about multiplying their magnitudes and adding their phases.

Raising a Complex Number to $M^{\text{th}}$ Power

Another consequence of the definition of complex multiplication described above is that raising a complex number $V$ to a power, say $2$, generates
\begin{equation*}
\begin{aligned}
|W| &= |V|.|V| = |V|^2 \\
\measuredangle W &= \measuredangle V +\measuredangle V = 2 \cdot \measuredangle V
\end{aligned}
\end{equation*}
For a general power $M$,
\begin{equation}
\begin{aligned}\label{eqIntroductionComplexRaisingM}
|W| &= |V|^M \\
\measuredangle W &= M \cdot \measuredangle V
\end{aligned}
\end{equation}
We can conclude that in an $IQ$-plane, raising a complex number to a certain power raises the magnitude to that power while multiplies the phase with that number.

Phase Rotation

Rotating a complex number in $IQ$-plane by a phase $\theta$ seems very simple in complex notation but a bit complicated in $IQ$ terms. Rotation implies keeping the magnitude constant and adding $\theta$ to the angle of that complex number, as shown in the figure below.

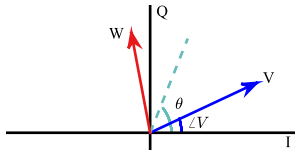
To start, let us multiply a complex number $V$ by a complex number $U$ with magnitude $1$ and angle $\theta$. Using $|U| = 1$ and $\measuredangle U = \theta$,
\begin{equation*}
U_I = \cos \theta \quad and \quad U_Q = \sin \theta
\end{equation*}
Hence,
\begin{equation}
\begin{aligned}\label{eqIntroductionPhaseRotation}
W_I\: &= V_I \cdot \cos \theta – V_Q \cdot \sin \theta \\
W_Q &= V_Q \cdot \cos \theta + V_I \cdot \sin \theta
\end{aligned}
\end{equation}
Using $V_I = |V| \cos \measuredangle V$ and $V_Q = |V| \sin \measuredangle V$,
\begin{equation*}
\begin{aligned}
W_I\: &= |V| \left(\cos \measuredangle V \cdot \cos \theta – \sin \measuredangle V \cdot \sin \theta \right) \\
W_Q &= |V| \left( \sin \measuredangle V \cdot \cos \theta + \cos \measuredangle V \cdot \sin \theta \right)
\end{aligned}
\end{equation*}
Again using the identities $\cos A \cos B – \sin A \sin B = \cos (A+B)$ and $\sin A$ $\cos B$ $+$ $\cos A \sin B = \sin (A+B)$,
\begin{equation}
\begin{aligned}\label{eqIntroductionPhaseRotated}
W_I\: &= |V| \cos \left(\measuredangle V + \theta \right) \\
W_Q &= |V| \sin \left(\measuredangle V + \theta \right)
\end{aligned}
\end{equation}
which keeps the magnitude unchanged and adds the angle $\theta$ to the existing angle. An algorithm known as Coordinate Rotation Digital Computer (CoRDiC) can be employed to implement phase rotations in an efficient manner.

A fast rule for phase rotation can be devised as follows. For a complex number $V$ and an angle $+\theta$ (i.e., counterclockwise rotation), the phase rotation rule states that

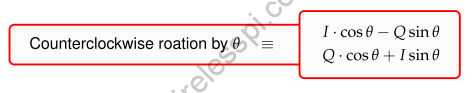
Similarly, for a complex number $V$ and an angle $-\theta$ (i.e., clockwise rotation)

The phase rotation rule above is important because we are not using complex notation in this text. That implies having on our disposal a quick way to recognize an equation if it rotates a complex number by an angle. The above two equations help fulfill that purpose.

Conjugate

The conjugate $V^*$ of a complex number $V$ is defined as
\begin{align*}
\{V ^*\}_I\: &= V_I \\
\{V ^*\}_Q &= -V_Q
\end{align*}

Since magnitude is the sum of squares of $I$ and $Q$ components, it remains unchanged. On the other hand, phase is $Q$ divided by $I$ which leads to the following definition of the conjugate of a complex number.
\begin{equation}
\begin{aligned}\label{eqIntroductionConjugate2}
|V^*| &= |V| \\
\measuredangle V^* &= – \measuredangle V
\end{aligned}
\end{equation}

A significance of conjugate of a complex number arises from the fact that a complex number multiplied by its complex conjugate cancels the phase and produces its magnitude squared. Using the above relations in multiplication rule,
\begin{equation*}
\begin{aligned}
\{V\cdot V^*\}_I\: &= V_I\cdot V_I – V_Q \cdot \left(-V_Q\right) \\
\{V\cdot V^*\}_Q &= V_Q\cdot V_I + V_I\cdot \left(-V_Q\right)
\end{aligned}
\end{equation*}
which generates the following result.
\begin{equation*}
\begin{aligned}
\{V\cdot V^*\}_I\: &= V_I^2 + V_Q^2 \\
\{V\cdot V^*\}_Q &= 0
\end{aligned}
\end{equation*}
Utilizing the definitions of magnitude and phase of complex numbers,
\begin{equation}
\begin{aligned}\label{eqIntroductionConjugateMultiply}
|V\cdot V^*| &= |V|^2 \\
\measuredangle \left(V\cdot V^*\right) &= 0
\end{aligned}
\end{equation}

Another interesting consequence of defining the conjugate of a signal is the following identity set.
\begin{equation*}
\begin{aligned}
\{V + V^*\}\: &= V_I + V_I = 2 V_I\\
\{V + V^*\} &= V_Q – V_Q = 0
\end{aligned}
\end{equation*}
which generates the following important results.
\begin{equation*}
\begin{aligned}
V_I &= \frac{1}{2}\left\{V+V^* \right\} \\
0 &= \frac{1}{2}\left\{V+V^* \right\}
\end{aligned}
\end{equation*}
On the same note,
\begin{equation*}
\begin{aligned}
0 &= \frac{1}{2}\left\{V-V^* \right\} \\
V_Q &= \frac{1}{2}\left\{V-V^* \right\}
\end{aligned}
\end{equation*}