Tag: Discrete Fourier Transform (DFT)

Projections of a sphere in Flatland
DSP / Wireless/SDR

Two Birds with One Tone: I/Q Signals and Fourier Transform – Part 2

In Part 1 of I/Q signals series, we saw the implications of orthogonality in amplitude and phase shift. This led to our treatment of signals as two dimensional complex numbers in time I/Q plane. Now we talk about orthogonality in frequency, how it gives rise to a different I/Q plane and see its implications in signal processing applications. Let us start with a new perspective that will lift more veils from the I/Q puzzle. A Basic Building Block Humans use the power of logic to uncover the rules according to which the world works. But our minds struggle to retain

Continue reading
Orange vs tangerine
DSP

The Fourier Doppelgangers

It is well known that Fourier Transform is unique under certain conditions that are satisfied by almost all practical signals. Then, how can we resolve the following contradiction? Consider a sinc pulse and Linear Frequency Modulated (LFM) pulse (a chirp) in time domain. The sinc pulse is defined as \[ \text{sinc}(t) = \frac{sin(\pi t)}{\pi t} \] Now the spectrum of a sinc pulse in time in an ideal case is a rectangular signal in frequency domain, which is the most fundamental relation in signal processing. Both the sinc pulse and its spectrum are plotted in the left half of the

Continue reading
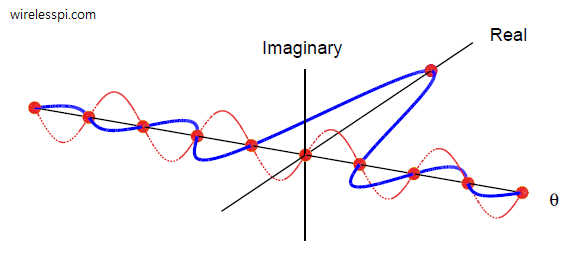
Discrete Fourier Transform (DFT) of a DFT-even sequence
DSP

The Beauty of Symmetry in Fourier Transform

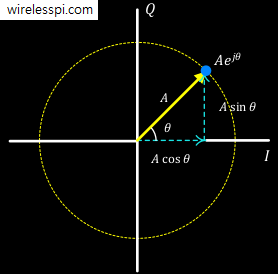
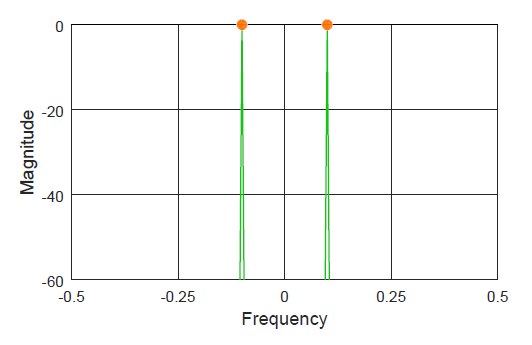
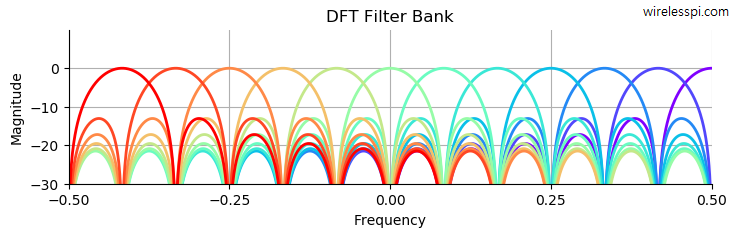
In 1978, Fred Harris was a relatively unknown faculty member at the San Diego State University when he published his landmark paper titled On the use of windows for harmonic analysis with the discrete Fourier transform. That paper made him a superstar in DSP community. It presented a brief overview of signal windows and their impact on the detection of harmonic signals in the presence of broad-band noise and nearby harmonic interference. More importantly, he pointed out several common errors in the application of windows when used in the context of Discrete Fourier Transform (DFT). Today I am going to

Continue reading
A complex number
DSP

Convolution and Fourier Transform

One question I am frequently asked is regarding the definition of Fourier Transform. A continuous-time Fourier Transform for time domain signal $x(t)$ is defined as \[ X(\Omega) = \int _{-\infty} ^{\infty} x(t) e^{-j\Omega t} dt \] where $\Omega$ is the continuous frequency. A corresponding definition for discrete-time Fourier Transform for a discrete-time signal $x[n]$ is given by \[ X(e^{j\omega}) = \sum _{n=-\infty} ^{\infty} x[n] e^{-j\omega n} \] where $\omega$ is the discrete frequency related to continuous frequency $\Omega$ through the relation $\omega = \Omega T_S$ if the sample time is denoted by $T_S$. Focusing on the discrete-time Fourier Transform for

Continue reading
Spectrum of a sinusoid
DSP

Generating Signals and Viewing the Spectrum

One of the most common questions DSP beginners have is how to generate the signals (particularly, sinusoids) and view their spectrum. They have a rough idea what time domain and frequency domain are about but struggle to construct the first few lines of code that open the gates towards a deeper understanding of signals. For this reason, I produce below an Octave (or Matlab) code that you can simply copy and paste to view and modify the results. Keep in mind that the code has been written for an explanation purpose, not conciseness or optimization. As you progress towards developing

Continue reading