Discrete Fourier Transform (DFT) Archives | Page 2 of 4

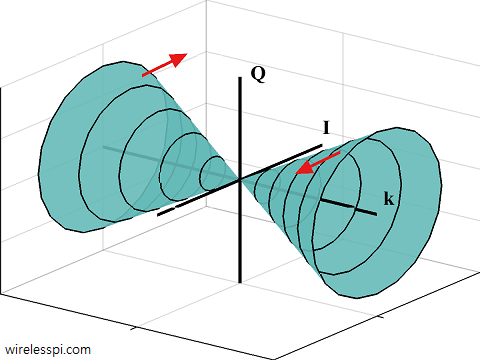
Symbolic representation of linear phase rotation that changes with frequency index

May 14, 2019 DSP

Effect of Time Shift in Frequency Domain

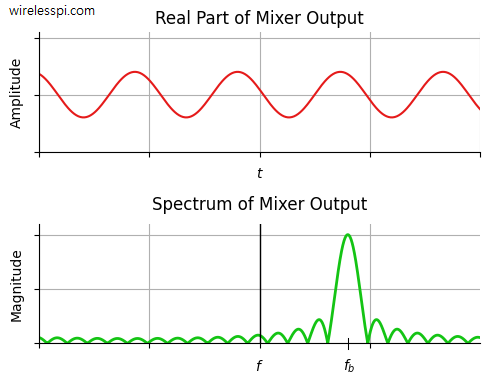
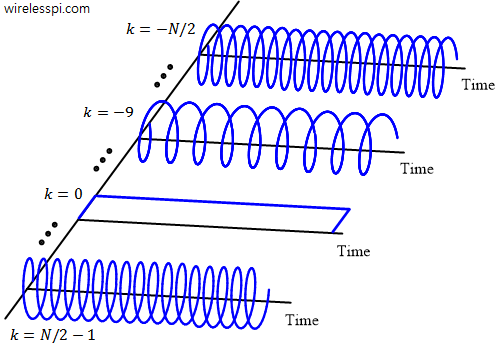
Children usually ask questions like “How many hours have passed?” And they have no idea about the start time to be taken as a reference. Just like the zero of a measuring tape, a zero reference for time plays a crucial role in analyzing the signal behaviour in time and frequency domains. Until now, we assumed that reference time $0$ coincides with the start of a sine and a cosine wave to understand the frequency domain. Later, we will deal with symbol timing synchronization problem in single-carrier systems and carrier frequency synchronization problem in multicarrier systems, both of which address

OFDM slices the spectrum just like a bread

May 1, 2017 Wireless/SDR

A Beginner’s Guide to OFDM

In the recent past, high data rate wireless communications is often considered synonymous to an Orthogonal Frequency Division Multiplexing (OFDM) system. OFDM is a special case of multi-carrier communication as opposed to a conventional single-carrier system. The concepts on which OFDM is based are so simple that almost everyone in the wireless community is a technical expert in this subject. However, I have always felt an absence of a really simple guide on how OFDM works which can prove useful for technical persons not wanting to deal with too much technicalities, such as DSP experts outside communications, computer programmers, ham

Beat frequency sinusoid and its spectrum

October 31, 2023 DSP

Spectrum of a Sinusoid

In this article, we derive the spectrum of a complex sinusoid that acts as the basis for all spectra. In fact, the very definition of the Fourier Transform, whether continuous or discrete, comes from the perspective of a complex sinusoid. Therefore, exploring this derivation will be useful in everything else we learn about DSP. For an in-depth understanding of complex signals and I/Q processing, you can read the following two articles (the option of downloading them as PDF is available). The origin of complex numbers and signals I/Q signal processing Let us start with the continuous-time case. A Continuous-Time Sinusoid

August 26, 2016 DSP

The Concept of Frequency

A wireless signal from one device to another travels through the use of electromagnetic waves propagated by an antenna. Electromagnetic waves have different frequencies and one can pick up a specific signal by tuning a radio Rx to a specific frequency. But what is a frequency anyway? Watch the video below for an interesting description of actual time domain samples and how to interpret their frequency domain representation. A Complex Sinusoid Consider a complex number $V$ in an $IQ$-plane. A complex number is defined as a pair of real numbers in $(x,y)$-plane similar to the vectors but with different arithmetic

August 18, 2016 DSP

Discrete Frequency

An Analog to Digital Converter (ADC) samples a continuous-time signal to produce discrete-time samples. For a digital signal processor, this signal just resides in memory as a sequence of numbers. Consequently, the knowledge of the sample rate $F_S$ is the key to signal manipulation in digital domain. As far as time is concerned, one can easily determine the period or frequency of such a signal stored in the memory. For example, the period $T$ in the sinusoid of Figure below is clearly $10$ samples and sample time $T_S=1/F_S$ can be employed to find its period in seconds. For a sample