Numerically Controlled Oscillator (NCO) Archives

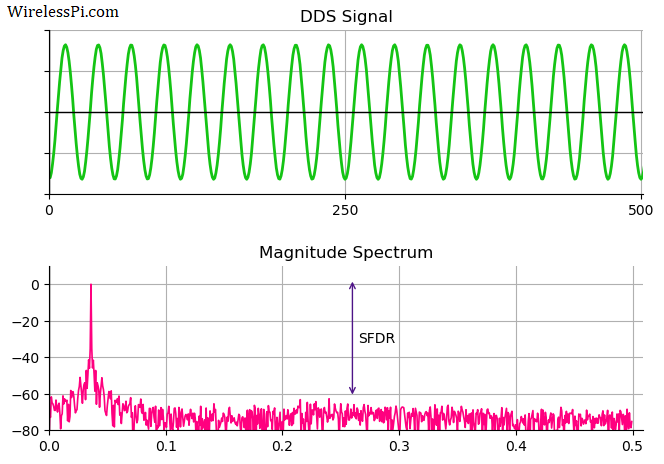
DDS waveform and spectrum after dithering

January 31, 2023 DSP / Wireless/SDR

Direct Digital Synthesizer (DDS)

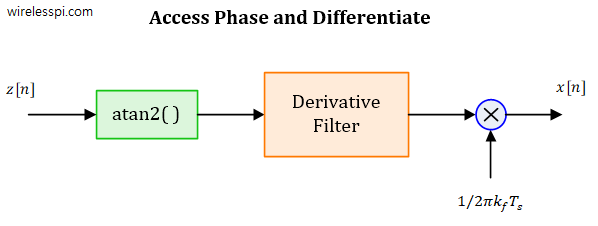
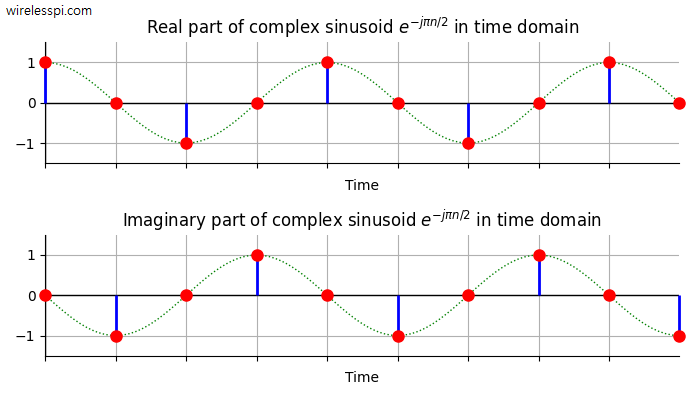
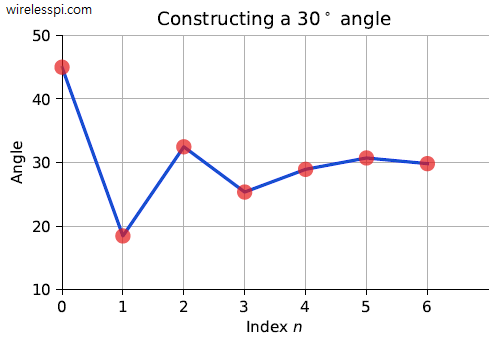
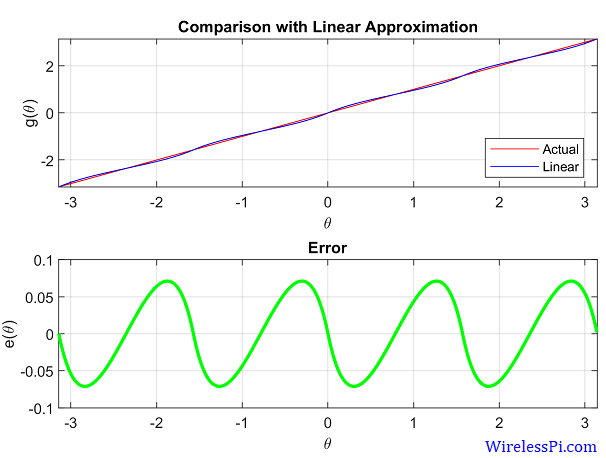
A Direct Digital Synthesizer (DDS) is an integral part of all modern communication systems. It is a technique to produce a desired waveform, usually a sinusoid, through employing digital signal processing algorithms. As an example, in the transmitter (Tx) of a digital communication system, a Local Oscillator (LO) is required to generate a carrier sinusoid that upconverts the modulated signal to its allocated frequency in the spectrum. On the receive (Rx) side, another local oscillator downconverts this high frequency signal to baseband for further processing. Such a process is shown in the Tx and Rx block diagrams of a Quadrature

A discrete-time FM demodulator block diagram with atan2 and derivative filter

December 8, 2022 DSP / Wireless/SDR

Frequency Modulation (FM) and Demodulation Using DSP Techniques

Frequency Modulation (FM) is as old as the history of wireless communications itself. The past few decades saw the rise of digital signal processing in all spheres of life that pervaded even the implementation of analog modulation schemes. Today many of the FM systems are built using discrete-time techniques instead of the conventional circuitry as described below. Frequency Modulation In digital communications, data is sent through altering a characteristic of an electromagnetic wave such as amplitude, frequency or phase in discrete steps (e.g., $M$ number of levels). Such systems are known as Amplitude Shift Keying (ASK), Frequency Shift Keying (FSK)

August 1, 2022 DSP

Spectral Shift without any Multiplications

One of the great advantages of Digital Signal Processing (DSP) is an unexpected simplification of operations in seemingly complicated scenarios. See the Cascade Integrator Comb (CIC) filters for how to accomplish the task of sample rate conversion along with filtering with minimal resources. As another example, in wireless communications and many other applications, a frequency translation is often required in which the spectrum of a signal centered at a particular frequency needs to be moved to another frequency. From the properties of Fourier Transform, a shift by frequency $\omega_0=2\pi F_0$ requires sample-by-sample multiplication with a complex sinusoid $e^{j\omega_0 t}$. \[

February 7, 2022 Wireless/SDR

Coordinate Rotation Digital Computer (CoRDiC)

Digitial Signal Processing (DSP) plays a crucial role in algorithm implmentation for building digital and wireless communication systems. A common theme in all those algorithms is that they can be implemented with the following simple operations: addition multiplication shift In fact, these are the basic principles on which a digital signal processor is constructed. However, when it comes to implementation of real-time systems in hardware such as FPGAs, we find ways to reduce the complexity even further. Which operation (out of the above three) do you think is the most demanding in computations? It is the multiplications. Therefore, it is

June 16, 2023 DSP

3 Ways to Approximate atan2( ) in Hardware

When we think about signal processing, the focus is usually magnitude response of a system. However, in several DSP applications, the signal phase holds as much, if not more, significance as the magnitude response. For example, in digital FM demodulation, carrier phase synchronization and RF ranging, the phase (found through arctangent in four quadrants) of a complex signal needs to be computed by an FPGA or a DSP for further processing. In image processing applications, such an operation is also required to calculate the gradient orientations used in several popular feature descriptors like the Scale-Independent Feature Transform (SIFT) or the