Downsampling Archives

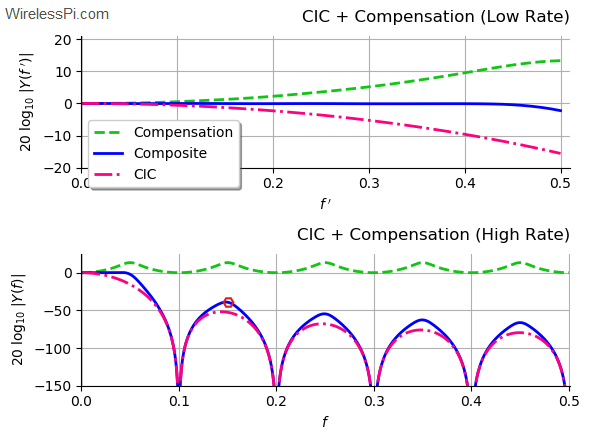
Spectrum of the cascade of CIC filters with a wideband compensation filter for rate change factor 10, unit differential delay and 4 stages

November 24, 2022 DSP / Wireless/SDR

Cascaded Integrator Comb (CIC) Filters – A Staircase of DSP

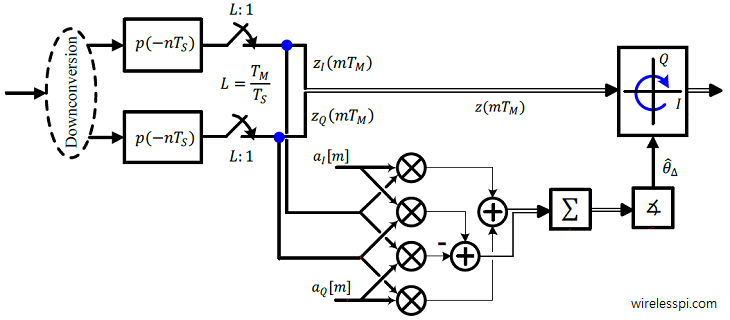
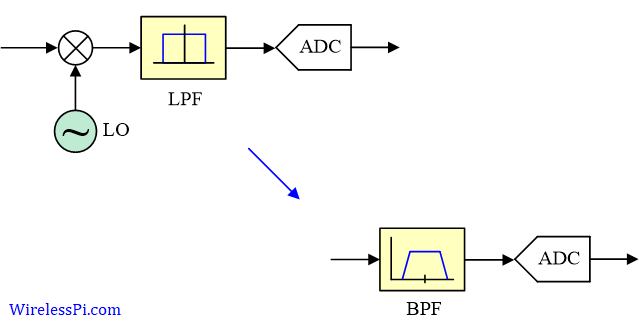
In olden days, people used to have lots of kids. A famous Urdu satirist once wrote: "It has been observed that the last kid is usually the most mischievous of them all. Therefore, there should be no last kid in a family!" I remembered this line today because I have observed that starting a write-up is the most difficult task of them all. Therefore, there is no introductory paragraph in this article. Suffice it to say that this is the only topic I have found that takes you from a very small first step (just two additions) to really advanced

A block diagram for the implementation of the feedforward phase estimator

September 24, 2019 Wireless/SDR

How to Estimate the Carrier Phase

In this article, I will describe how to estimate the carrier phase from an incoming waveform in a feedforward manner. This algorithm utilizes a sequence of known pilot symbols embedded within the signal along with the unknown data symbols. Such a signal is sent over a link in the form of separate packets in burst mode wireless communications. In most such applications with short packets, the phase offset $\theta_\Delta$ remains constant throughout the duration of the packet and a single shot estimator is enough for its compensation. Here, the primary task of the designer is to develop this closed-form expression

October 24, 2022 DSP

On Analog-to-Digital Converter (ADC), 6 dB SNR Gain per Bit, Oversampling and Undersampling

We have discussed before the sampling on time axis for analog to digital (A/D) conversion. An Analog to Digital Converter (ADC) produces the samples $x[n]$ of a continuous-time signal $x(t)$ at its input. Ideally, these samples are the exact values of the signal $x(t)$ at time instants $nT_s$ where $T_s=1/f_s$ is the sampling period. In practice, however, there are imperfections both on the y-axis and the x-axis. On y-axis, an ADC has a finite resolution depending on the number of bits used for quantization. On x-axis, there are issues of clock jitter that distort the samples produced. In this article,

Eye diagram for a 4-QAM modulated signal and a simple channel impulse response

December 30, 2016 Wireless/SDR

Impact of Multipath on the Received Signal

In this article, we describe the impact of multipath caused by the wireless channel on the signal arriving at the receiver from a constellation viewpoint. Recall that an eye diagram, a transition diagram and a scatter plot are the stethoscopes of a communication system and hence it is imperative to bring in that perspective for a Tx signal convolved with the channel impulse response. This is because a wireless channel can be seen as a Finite Impulse Response (FIR) filter with the result that the sampled Rx signal is a convolution between taps of this FIR filter and the Tx

November 15, 2016 DSP

Sampling and the Mysterious Scaling Factor

This post treats the signals in continuous time which is different than the approach I adopted in my book. The book deals exclusively in discrete time. Some time ago, I came across an interesting problem. In the explanation of sampling process, a representation of impulse sampling shown in Figure below is illustrated in almost every textbook on DSP and communications. The question is: how is it possible that during sampling, the frequency axis gets scaled by $1/Ts$ — a very large number? For an ADC operating at 10 MHz for example, the amplitude of the desired spectrum and spectral replicas