Pulse Shaping Archives

November 18, 2021 Wireless/SDR

How Do Beams Look Like?

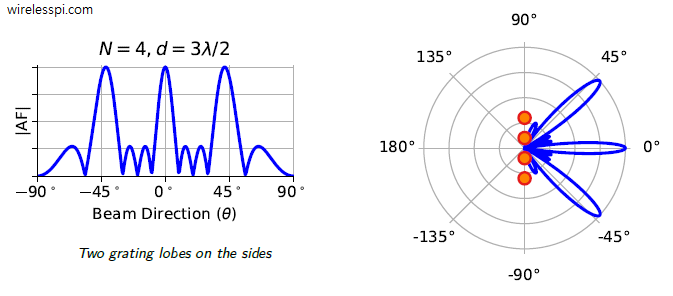
In the article on beamforming, we discussed the interaction of the electromagnetic waves with the antenna array without any description of what the beam shape looks like. As we explore below now, the beam shape is given by the Fourier Transform of individual antenna intensities but the reason behind this is not always explained in most of the textbooks and tutorials on this topic. Where exactly does the Fourier Transform, a conversion tool from time $t$ to frequency $\omega=2\pi F$ domain, come into the picture? And how does the frequency $\omega$ for time domain correspond to phase shift $u$ of

Odd symmetry around frequency points at half symbol rate adding up to a flat spectrum

February 29, 2024 DSP / Wireless/SDR

Proof of Poisson Sum Formula

The Poisson sum formula was discovered by the French mathematician and physicist Siméon Denis Poisson. It has several applications in digital signal processing, among which our concern is the periodic summation of modulated pulses in digital communication systems. Assume that $p(t)$ is a pulse shape (or any continuous-time function if you are not familiar with digital communications) and $P(f)$ is its Fourier Transform. The pulse is sampled at a rate of $f_s$ to produce its discrete version $p(nT_s)$ where $T_s=1/f_s$ is the duration between two samples. The Poisson summation formula relates these two quantities as \begin{equation}\label{equation-poisson-sum-formula} \frac{1}{T_s}\sum _{k=-\infty}^{\infty} P\left(f+\frac{k}{T_s}\right) =

At the boundary of two OFDM symbols, pulse shaping smoothes the edges, resulting in the avoidance of spectral regrowth

February 26, 2020 Wireless/SDR

Windowing an OFDM Signal in Time Domain

Orthogonal Frequency Division Multiplexing (OFDM) has been introduced in a previous article as a technique suitable for high data-rate transmissions over a wireless channel. The two main advantages I mentioned were as follows: Simple one-tap equalization, and Ability to slice the spectrum and utilize each slice in an independent manner. Due to these advantages, it was adopted as the preferred modulation in WiFi and 4G-LTE systems. The interesting part is that while many new waveforms were proposed to replace it in 5G NR, OFDM was still the modulation of choice for both downlink and uplink directions with some minor changes.

Square-root Nyquist filters for three different excess bandwidths

September 16, 2017 DSP / Wireless/SDR

How to Design Nyquist and Square-Root Nyquist Pulse Shaping Filters

The radio spectrum is a very precious resource like real estate and must be utilized judiciously. Pulse shaping filters control the spectral leakage of the transmitted signal in a wireless channel due to the strict restrictions to comply with a spectral mask. This is even more important for the upcoming 5G wireless systems which are based on a variety of wireless transmission protocols (such as mobile networks, Internet of Things (IoT) and machine to machine communications) combined in one comprehensive standard. Even for wired channels, there is always a natural bandwidth of the medium (copper wire, coaxial cable, optical fiber)

A matched filter in continuous frequency domain along with the corresponding frequency matched filter for excess bandwidth 0.25

September 10, 2016 DSP / Wireless/SDR

Band Edge Filters for Carrier and Timing Synchronization

Band edge filters for carrier frequency and symbol timing synchronization is a very interesting topic that elegantly relates the tool (DSP) to the application (SDR design). This article is a short summary of where they originate from and what role they play for synchronization purpose. A Carrier Frequency Offset (CFO) arises due to a mismatch between Tx and Rx local oscillators as well as a phenomenon known as Doppler effect. In some other articles on this website, you will also find information on the Phase Locked Loop (PLL) in the context of carrier phase and timing synchronization. There is another