Proof of Poisson Sum Formula

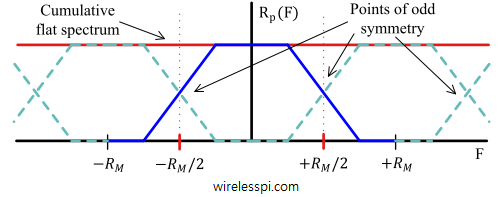
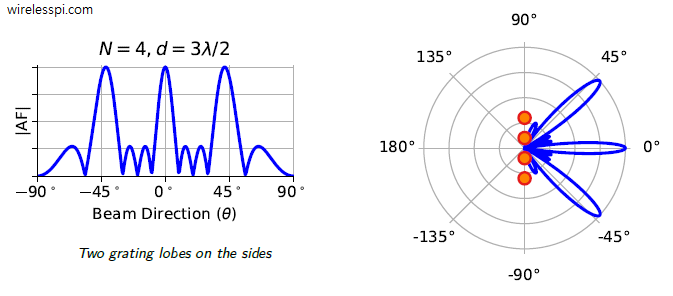
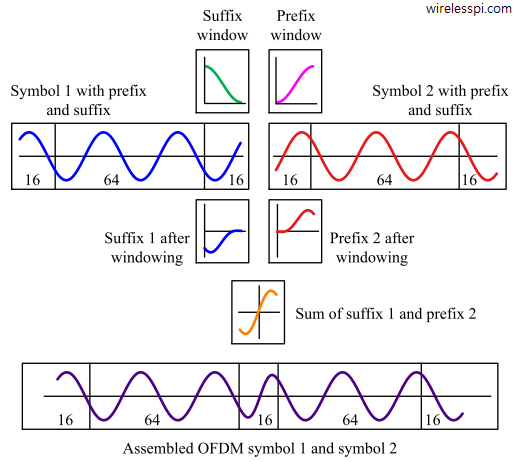
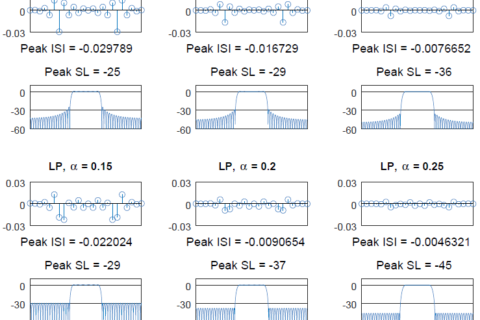
The Poisson sum formula was discovered by the French mathematician and physicist Siméon Denis Poisson. It has several applications in digital signal processing, among which our concern is the periodic summation of modulated pulses in digital communication systems.

Assume that $p(t)$ is a pulse shape (or any continuous-time function if you are not familiar with digital communications) and $P(f)$ is its Fourier Transform. The pulse is sampled at a rate of $f_s$ to produce its discrete version $p(nT_s)$ where $T_s=1/f_s$ is the duration between two samples. The Poisson summation formula relates these two quantities as

The easiest proof of this equation comes from writing the mathematical expression of the sampling process which transforms the continuous-time pulse shape $p(t)$ into a discrete-time sequence $p(nT_s).$ Sampling a signal at intervals of $T_s$ seconds is represented as its multiplication with a sequence of unit impulses $\delta (t)$, which is known as an impulse train.

Therefore, the starting point is an intermediate signal $x(t)$ given by
\begin{equation}\label{equation-x-intermediate}
x(t) = p(t) \sum _{n=-\infty}^{\infty} \delta(t-nT_s)
\end{equation}

From this expression, we can derive both the left and right hand sides of Eq (\ref{equation-poisson-sum-formula}).

• RHS: Applying the definition of Fourier Transform to $x(t)$ in Eq (\ref{equation-x-intermediate}) above, we get
  \[
  X(f) = \int _{-\infty}^{\infty} x(t) e^{-j2\pi ft}dt = \int _{-\infty}^{\infty} p(t) \sum _{n=-\infty}^{\infty} \delta(t-nT_s) e^{-j2\pi ft}dt
  \]

  Owing to linearity of Fourier Transform, we can interchange the order of integration and summation.
  \[
  X(f) = \sum _{n=-\infty}^{\infty} \int _{-\infty}^{\infty} p(t) \delta(t-nT_s) e^{-j2\pi ft}dt
  \]

  Since these unit impulses only exist at locations $t=nT_s$ and nowhere else and the area under each such impulse is $\int _{-\infty}^{\infty}\delta(t)=1$, we can write
  \[
  X(f) = \sum _{n=-\infty}^{\infty} p(nT_s) e^{-j2\pi fnT_s}dt
  \]

  This operation is known as the sifting property of the unit impulse. We have arrived at the RHS of the Poisson sum formula in Eq (\ref{equation-poisson-sum-formula}).

• LHS: Trace the following steps to derive the LHS. Notice that Eq (\ref{equation-x-intermediate}) is a multiplication between $p(t)$ and an impulse train $\sum _{n=-\infty}^{\infty} \delta(t-nT_s)$.
  1. Fourier Transform of a time domain impulse train is another impulse train in frequency domain given by
     \[
     \sum _{n=-\infty}^{\infty} \delta(t-nT_s) \quad \leftrightarrow \quad \frac{1}{T_s}\sum _{k=-\infty}^{\infty} \delta\left(f-\frac{k}{T_s}\right)
     \]

  2. Multiplication of two operations in time domain is their convolution in frequency domain.
  3. As a consequence, we can write the Fourier Transform $X(f)$ as
     \[
     X(f) = P(f) * \frac{1}{T_s}\sum _{k=-\infty}^{\infty} \delta\left(f-\frac{k}{T_s}\right)
     \]

     Since convolution of a signal with a unit impulse $\delta(f-f_0)$ is the same signal shifted at $f_0$, we get
     \[
     X(f) = \frac{1}{T_s}\sum _{k=-\infty}^{\infty} P\left(f-\frac{k}{T_s}\right)
     \]

     A plus or minus sign with the index term $k/T_s$ simply returns the same summation. Hence, we have arrived at the LHS in Eq (\ref{equation-poisson-sum-formula}).

This completes the proof of the Poisson sum formula.