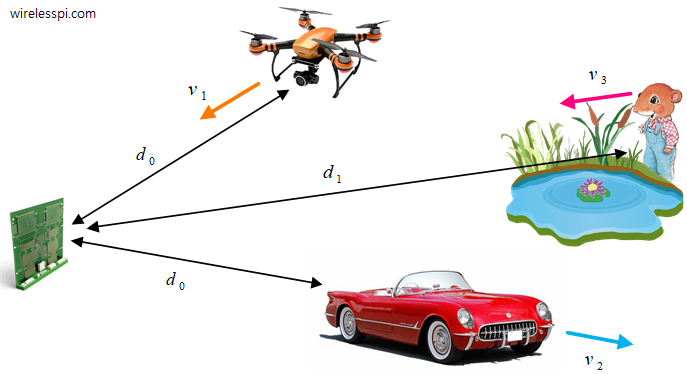
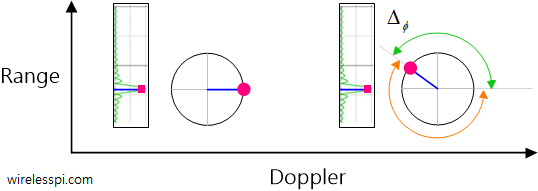
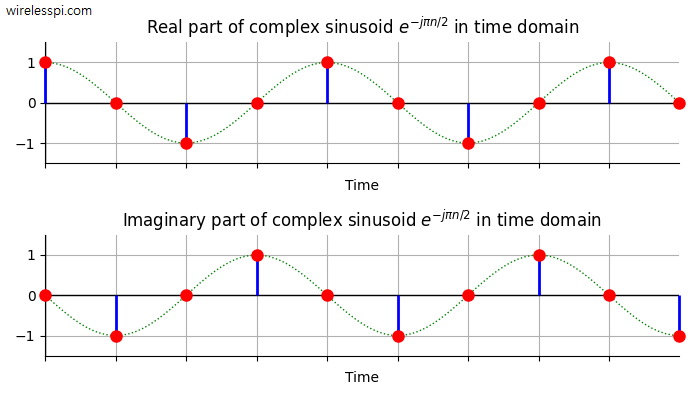
When a new member arrives at the DSP club, this is what they find at the club gate: I/Q signals. Perhaps a secret plot to keep most people out of the party? Some return from here to try another area (e.g., machine learning, which pays more and is easier to understand but less interesting than DSP). Others persist enough to push the gate open (even a little understanding is sufficient for this task). So what exactly makes this topic so mysterious? To investigate the answer, we start with an example audio signal drawn in the figure below that displays amplitude
Continue reading