Complex Sinusoids Archives | Page 3 of 4

March 25, 2024 DSP / Miscellaneous

Why the Constant e Arises in Complex Plane as a Rotation

In the tutorial on how complex numbers arose, we asked three questions. The first two were answered in the same article while the answer to the third question, repeated below, is explained here. Why is the expression $e^{i \theta}$ a rotation of 1 by $\theta$ radians on a unit circle? Is it possible to make sense out of a number like $2.71828^{\sqrt{-1}\cdot\theta}$? The constant e is a special number discovered by Jacob Bernoulli while studying compound interests. It appears in many other forms as well which are all related to each other but that topic is a complete account in

Plots for positive integer powers of x in 3D

June 26, 2020 DSP / Miscellaneous

A Real-Imaginative Guide to Complex Numbers

June 18, 2020 On a cold morning in August 2015, I narrowly missed a train to my office in Melbourne city. With nothing else to do in the next 20 minutes, my mind wandered towards an intuitive view of complex numbers, something that has puzzled me since long. In particular, I wanted to seek answers to the following questions. (a) What is the role of the number $\sqrt{-1}$ in mathematics? What sets it apart from other impossible numbers, e.g., a number $k$ such that $|k|=-1$? (The origins of this question might lie in how I cut apple slices for my

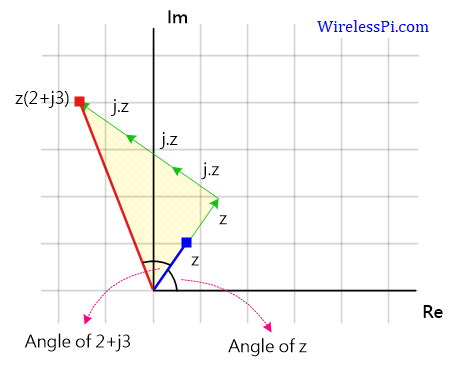
Intuition behind multiplying two complex numbers

March 14, 2025 Wireless/SDR

Intuitive Reason behind Multiplication and Division of Complex Numbers

Any introduction to complex numbers and their operations follows a common pattern: the formulas are given without building any intuition. If you have ever wondered about why $j=\sqrt{-1}$, you can read about the origin of complex numbers. In this article, I will explain the intuitive reason behind why a product of two complex numbers multiplies their magnitudes and adds their angles, and a division of two complex numbers divides their magnitudes and subtracts their angles. Let us start with the multiplication. The division scenario can be analogously derived with inverse operations. Multiplication of Complex Numbers The intuition behind multiplying two

Symbolic representation of linear phase rotation that changes with frequency index

May 14, 2019 DSP

Effect of Time Shift in Frequency Domain

Children usually ask questions like “How many hours have passed?” And they have no idea about the start time to be taken as a reference. Just like the zero of a measuring tape, a zero reference for time plays a crucial role in analyzing the signal behaviour in time and frequency domains. Until now, we assumed that reference time $0$ coincides with the start of a sine and a cosine wave to understand the frequency domain. Later, we will deal with symbol timing synchronization problem in single-carrier systems and carrier frequency synchronization problem in multicarrier systems, both of which address

December 22, 2017 DSP

Interpreting Time Domain Derivative in Frequency Domain

Although this article explains the concepts in terms of mathematical constants e and j as well as integration, my book on SDR steers clear of the complex notation and integrals to describe the underlying concepts from the ground up to an advanced level. One of the properties of Fourier Transform is that the derivative of a signal in time domain gets translated to multiplication of the signal spectrum by $j2\pi f$ in frequency domain. This property is usually derived as follows. For a signal $s(t)$ with Fourier Transform $S(f)$ \begin{equation*} s(t) = \frac{1}{2\pi}\int \limits _{-\infty}^{+\infty} S(f) e^{j2\pi ft}df, \end{equation*} we