Tag: FIR Filter

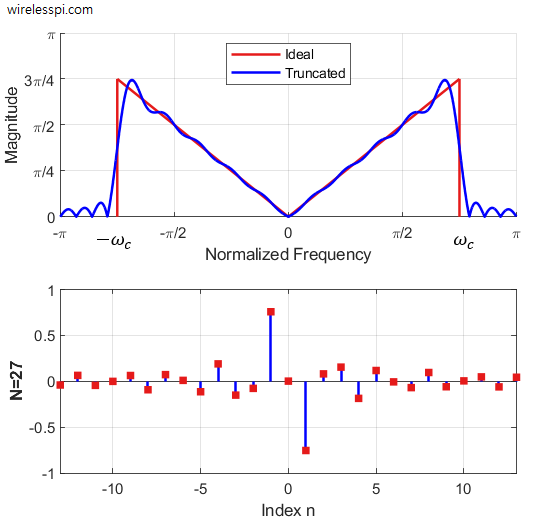
Wideband differentiator frequency and impulse responses
DSP

Design of a Discrete-Time Differentiator

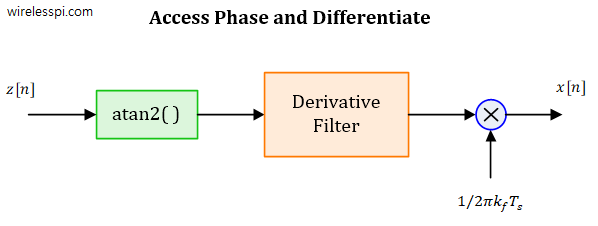
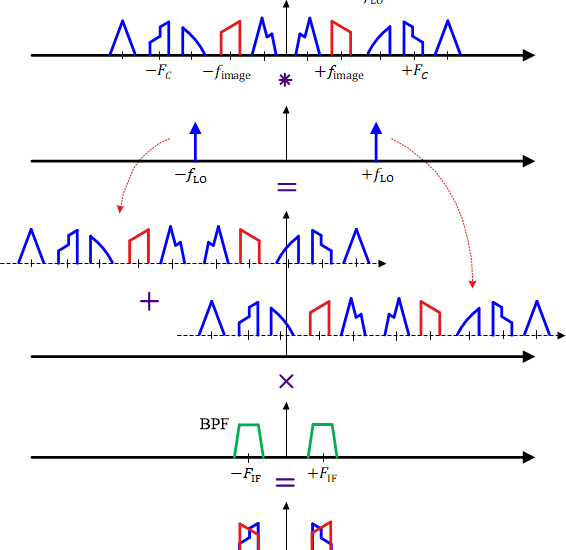
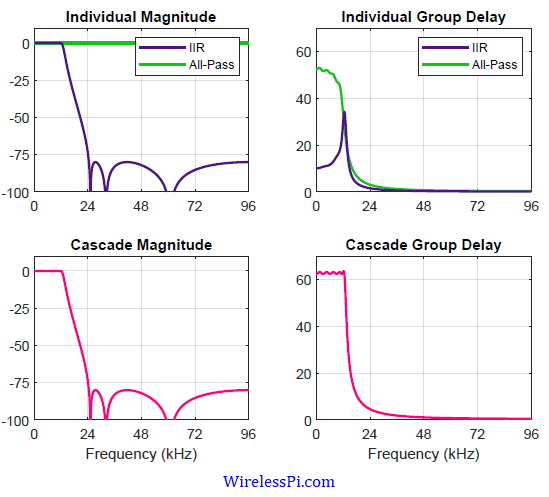
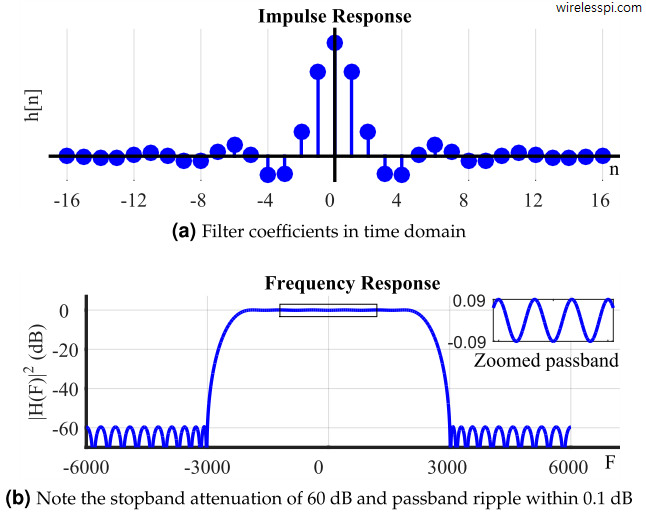
Many signal processing algorithms require computation of the derivative of a signal in real-time. Some of the examples are timing recovery, carrier frequency synchronization, FM demodulation and demodulation of LoRa signals. An analog or digital filter that computes such a derivative is known as a differentiator. Before we design such a discrete-time differentiating filter, let us review some of the fundamentals. A Derivative The following quote is attributed to Heraclitus, a Greek philosopher, from 535 BC. Change is the only constant in life. This was brought into the realm of science by Newton and Leibniz. The purpose of science is

Continue reading
A discrete-time FM demodulator block diagram with atan2 and derivative filter
DSP / Wireless/SDR

Frequency Modulation (FM) and Demodulation Using DSP Techniques

Frequency Modulation (FM) is as old as the history of wireless communications itself. The past few decades saw the rise of digital signal processing in all spheres of life that pervaded even the implementation of analog modulation schemes. Today many of the FM systems are built using discrete-time techniques instead of the conventional circuitry as described below. Frequency Modulation In digital communications, data is sent through altering a characteristic of an electromagnetic wave such as amplitude, frequency or phase in discrete steps (e.g., $M$ number of levels). Such systems are known as Amplitude Shift Keying (ASK), Frequency Shift Keying (FSK)

Continue reading
The image frequency problem of a superheterodyne Rx
Wireless/SDR

The Heterodyne Principle and the Superheterodyne Receiver

During World War I, Edwin Howard Armstrong invented the superheterodyne Rx as an alternative to the Tuned Radio Frequency (TRF) receivers that moved a tunable filter to the desired signal. His purpose was to overcome their limitations in regard to selectivity and sensitivity. To understand the principle of a heterodyne receiver, a pictorial representation is of utmost importance. While this is generally true for all concepts, there are specific issues of spectral translations in receiver architectures that require nice and clear figures. This is how I proceed below. The Heterodyne Principle Instead of employing a tunable bandpass filter that is

Continue reading
Individual and cascade frequency responses as well as group delays of the IIR and all-pass filters combination
DSP

FIR vs IIR Filters – A Practical Comparison

When it comes to practical applications, digital filter design is one of the most important topics in digital signal processing. Today we discuss a critical question encountered in filter design: how to compare the Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters. Since there is no clear winner, answering this question enables a designer to choose the right solution for their product. A brief comparison of FIR vs IIR filters is now explained below. Computational Complexity It is well known that most practical signals are simply sums of sinusoids. This implies that signals with sharp transition in time

Continue reading
Time and frequency response of a lowpass FIR filter designed with Parks-McClellan algorithm for N=33
DSP

Why FIR Filters have Linear Phase

One of the most attractive properties of a Finite Impulse Response (FIR) filter is that a linear phase response is easier to achieve. Not all FIR filters have linear phase though. This is only possible when the coefficients or taps of the filter are symmetric or anti-symmetric around a point. Today I want to describe the reason behind this kind of phase response in an intuitive manner. We have described Finite Impulse Response (FIR) filters before. Moreover, we have also discussed that the Discrete Fourier Transform (DFT) of a signal is complex in general and therefore both magnitude and phase

Continue reading