FIR Filter Archives | Page 3 of 4

May 9, 2017 DSP

Moving Average Filter

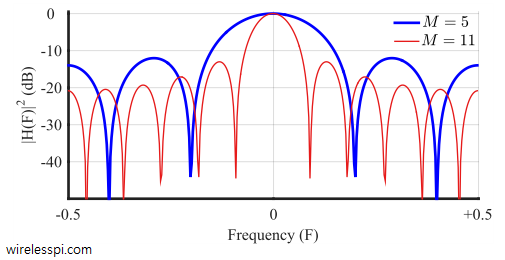
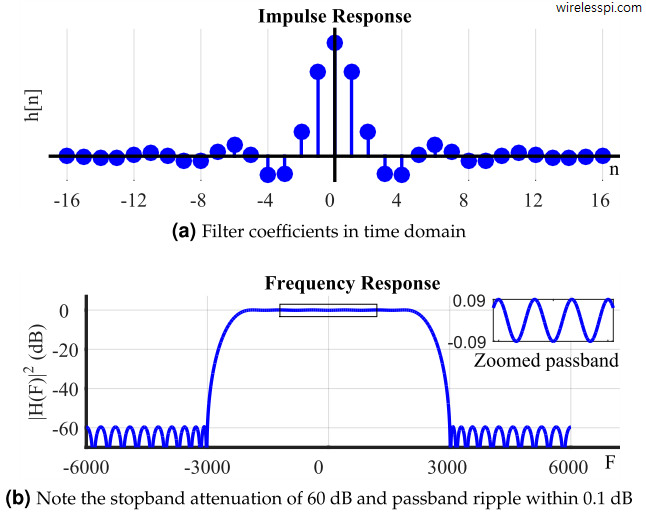
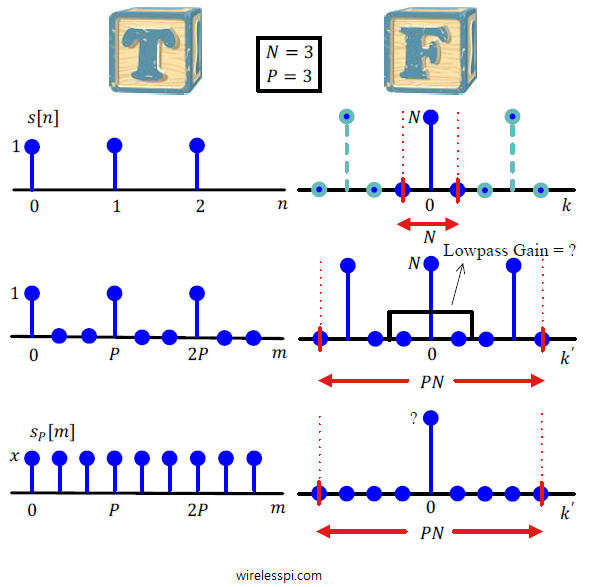
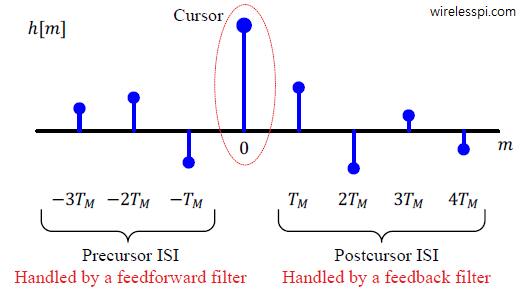
The most commonly used filter in DSP applications is a moving average filter. In today’s world with extremely fast clock speeds of the microprocessors, it seems strange that an application would require simple operations. But that is exactly the case with most applications in embedded systems that run on limited battery power and consequently host small microcontrollers. For noise reduction, it can be implemented with a few adders and delay elements. For lowpass filtering, an excellent frequency domain response and substantial suppression of stopband sidelobes are less important than having a basic filtering functionality, which is where a moving average

Eye diagram for a 4-QAM modulated signal and a simple channel impulse response

December 30, 2016 Wireless/SDR

Impact of Multipath on the Received Signal

In this article, we describe the impact of multipath caused by the wireless channel on the signal arriving at the receiver from a constellation viewpoint. Recall that an eye diagram, a transition diagram and a scatter plot are the stethoscopes of a communication system and hence it is imperative to bring in that perspective for a Tx signal convolved with the channel impulse response. This is because a wireless channel can be seen as a Finite Impulse Response (FIR) filter with the result that the sampled Rx signal is a convolution between taps of this FIR filter and the Tx

Time and frequency response of a lowpass FIR filter designed with Parks-McClellan algorithm for N=33

August 30, 2016 DSP

Finite Impulse Response (FIR) Filters

We learned in the concept of frequency that most signals of practical interest can be considered as a sum of complex sinusoids oscillating at different frequencies. The amplitudes and phases of these sinusoids shape the frequency contents of that signal and are drawn through magnitude response and phase response, respectively. In DSP, a regular goal is to modify these frequency contents of an input signal to obtain a desired representation at the output. This operation is called filtering and it is the most fundamental function in the whole field of DSP. It is possible to design a system, or filter,

A rectangular signal and its upsampled version in time and frequency domains

August 3, 2016 DSP

Sample Rate Conversion

In the discussion on sampling, the process of sampling a continuous-time signal was discussed in detail and subsequently sampling theorem was derived. In many applications, resampling an already digitized signal is mandatory for an efficient system design. In wireless communications, sample rate conversion is utilized for upconversion and downconversion to a desired frequency, filtering stages in the digital frontend and sometimes for carrier and timing synchronization during signal acquisition. See the Cascade Integrator Comb (CIC) filters for how to accomplish this task with minimal resources. In discrete domain, sample rate can be reduced by discarding intermediate samples periodically called downsampling

A channel with 8 taps demonstrating the main cursor, precursor ISI and postcursor ISI

January 31, 2022 Wireless/SDR

How Decision Feedback Equalizers (DFE) Work

We started the classification of equalization algorithms by introducing the need for equalization in wireless communication systems. We said that the wireless channel is a source of severe distortion in the received (Rx) signal and our main task is to remove the resulting Inter-Symbol Interference (ISI) from the Rx samples. Equalization refers to any signal processing technique in general and filtering in particular that is designed to eliminate or reduce this ISI before symbol detection. In essence, the output of an equalizer should be a Nyquist pulse for a single symbol case. A conceptual block diagram of the equalization process