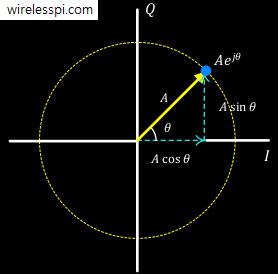
One question I am frequently asked is regarding the definition of Fourier Transform. A continuous-time Fourier Transform for time domain signal $x(t)$ is defined as \[ X(\Omega) = \int _{-\infty} ^{\infty} x(t) e^{-j\Omega t} dt \] where $\Omega$ is the continuous frequency. A corresponding definition for discrete-time Fourier Transform for a discrete-time signal $x[n]$ is given by \[ X(e^{j\omega}) = \sum _{n=-\infty} ^{\infty} x[n] e^{-j\omega n} \] where $\omega$ is the discrete frequency related to continuous frequency $\Omega$ through the relation $\omega = \Omega T_S$ if the sample time is denoted by $T_S$. Focusing on the discrete-time Fourier Transform for
Continue reading