Tag: Phase Recovery

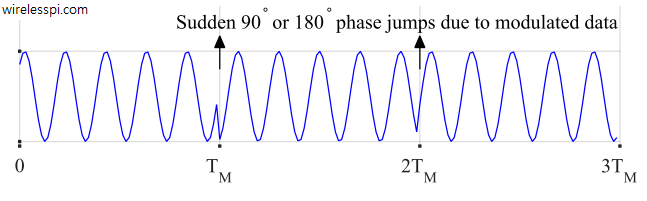
Phase jumps at every zero crossing from modulating data onto the carrier phase for a QPSK waveform
Wireless/SDR

The Fundamental Problem of Synchronization

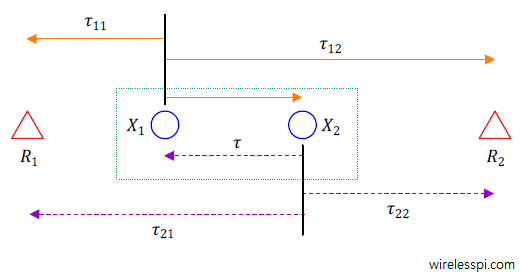
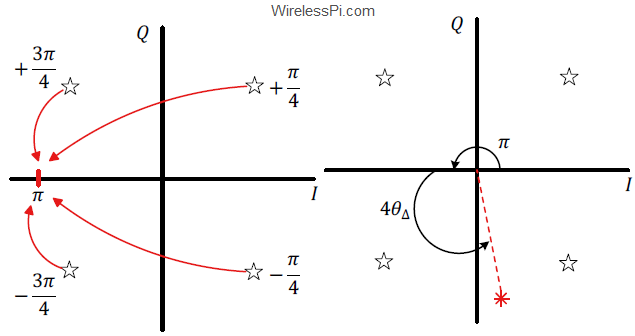
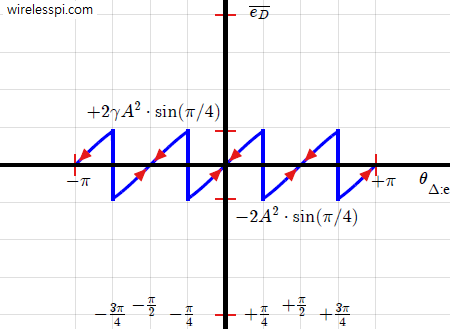
We have seen in the effect of phase rotation that the matched filter outputs do not map back perfectly onto the expected constellation, even in the absence of noise and no other distortion. Unless this rotation is small enough, it causes the symbol-spaced optimal samples to cross the decision boundary and fall in the wrong decision zone. And even for small rotations, relatively less amount of noise can cause decision errors in this case, i.e., noise margin is reduced. In fact, for higher-order modulation, the rotation becomes even worse because the signals are closely spaced with each other for the

Continue reading
A general QAM detector with respective waveforms at each block
Wireless/SDR

Quadrature Amplitude Modulation (QAM)

Quadrature Amplitude Modulation (QAM) is a spectrally efficient modulation scheme used in most of the high-speed wireless networks today. We discussed earlier that Pulse Amplitude Modulation (PAM) transmits information through amplitude scaling of the pulse $p(nT_S)$ according to the symbol value. To understand QAM, two routes need to be traversed. Route 1 We start the first route with differentiating between baseband and passband signals. A baseband signal has a spectral magnitude that is nonzero only for frequencies around origin ($F=0$) and negligible elsewhere. An example spectral plot for a PAM waveform is shown below for 500 2-PAM symbols shaped by

Continue reading
Setup for Differential Phase Difference of Arrival (DPDoA)
Localization

Location Estimation through Differential Phase Difference of Arrival

In an article on carrier phase based ranging, we saw how phase observations were employed to find the range between two wireless devices. Today we explore how phase can also be used for the purpose of location estimation. Background To determine the position of a wireless device, its range needs to be computed from a set of anchor nodes. When these anchors and the device itself are synchronized with each other, the signal propagation time of an electromagnetic wave arriving at these anchors after its emission from a Tx can be employed to calculate the corresponding distances. This is the

Continue reading
An illustration of wiping off the modulation process without any training information
Wireless/SDR

Non-Data-Aided Carrier Phase Estimation

A carrier phase offset rotates the Rx constellation causing decision errors even in a perfectly noiseless environment. One of the techniques used to overcome this problem is to insert a known sequence at the start of the transmission known as a preamble. Then, the Rx can utilize these known symbols in the arriving signal to estimate the carrier phase and de-rotate the constellation. However, inserting a known sequence within the message decreases the spectral efficiency of the system. To avoid this cost, a phase estimator (as well as estimators for other distortions) can be derived in a non-data-aided fashion. One

Continue reading
S-curve for decision-directed maximum likelihood phase error detector
Wireless/SDR

What are Cycle Slips and Hangup in Phase Locked Loops?

In a previous article, we have covered in detail the inner workings of a Phase Locked Loop (PLL) in a Software Defined Radio (SDR). There are two phenomena that have the potential to occasionally disrupt the performance of a PLL operating in steady state: cycle slips and hangup. Both the carrier and timing locked loops suffer from these issues. The underlying mathematics is quite intricate and hence I give a simple overview of these concepts. A reader interested in further exploration is referred to [1]. Cycle Slips To understand the cycle slip, assume that the loop is in tracking mode,

Continue reading