In a previous article, we have covered in detail the inner workings of a Phase Locked Loop (PLL) in a Software Defined Radio (SDR). There are two phenomena that have the potential to occasionally disrupt the performance of a PLL operating in steady state: cycle slips and hangup. Both the carrier and timing locked loops suffer from these issues. The underlying mathematics is quite intricate and hence I give a simple overview of these concepts. A reader interested in further exploration is referred to [1].
Cycle Slips
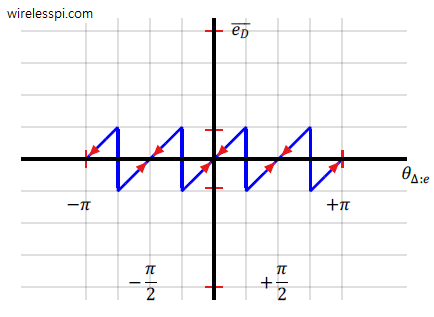
To understand the cycle slip, assume that the loop is in tracking mode, implying that its phase estimate is fluctuating around the true offset. At some instance, a noise spike can create a sudden large phase deviation from this equilibrium point such that its phase estimate gets attracted to another stable point (such as $-\pi/2$, $+\pi/2$ or $\pi$ in a decision-directed scenario, as shown in the figure below). The resultant phase correction in subsequent symbols will contain an additional multiple of $\pi/2$ thus ruining a series of symbol decisions in the future until a mechanism detects these errors, declares a failure and the loop reacquires the true phase.
Hangup
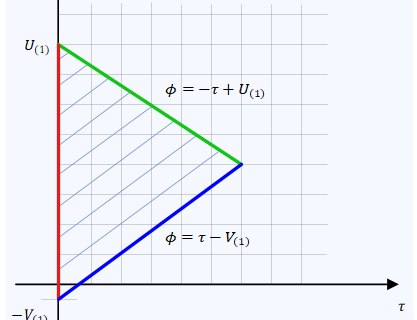
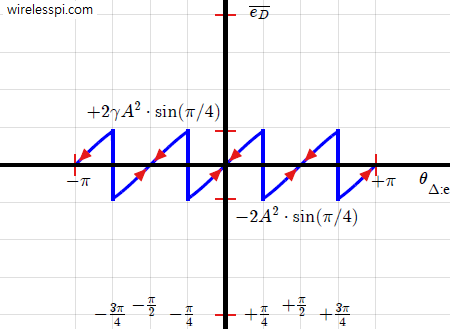
A problem that frequently appears during phase acquisition in a feedback structure is a hangup event. Assume that the initial value of the phase estimate is somewhere close to a negative slope zero, see the figure below. Although the system does have a tendency to move to a stable point as indicated by the directional arrows close to $\pm \pi$, the error signal around this location is small. This error signal is the main steering force behind acquisition but here it injects very marginal input into the subsequent blocks. As a consequence, the phase estimate may dwell around this position for a long time, considerably increasing the acquisition time. A long acquisition time renders a communication failure in many scenarios and is highly undesirable.

Hangup is specifically related to a feedback synchronization system like a PLL. A feedforward procedure does not suffer from this problem by virtue of generating a single estimate in an open loop.
References
[1] R. Best, Phase Locked Loops: Design, Simulation, and Applications, 6th Edition, McGraw Hill, 2007.