Tag: Probability

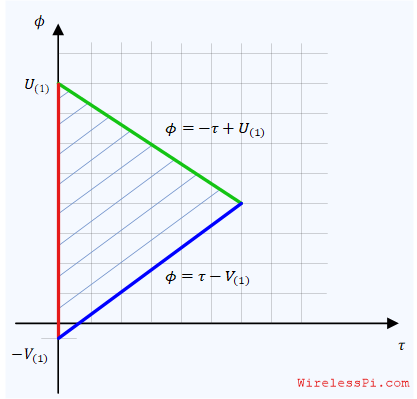
Region where likelihood function is non-zero
Wireless/SDR

Maximum Likelihood Estimation of Clock Offset

When I started my PhD, one of the first papers I read was On Maximum Likelihood Estimation of Clock Offset by Daniel Jeske [1] from University of California, Riverside. It eventually set the direction of my future research and ultimately my PhD dissertation. I found this paper quite interesting as it talked about the estimation of clock phase offset. Later I went on to explore what was missing here (the clock frequency offset) and more. Keep in mind that carrier phase estimation is a different problem that has already been discussed in the past here, here and here. Most of

Continue reading
Earth lies in the Goldilocks Zone of our solar system
Wireless/SDR

Diversity in Wireless Communication Systems

Diversity is one of those few ideas that are extremely dumb and extremely clever at the same time. It can be explained in one sentence as well as in a whole book. The basic idea, nevertheless, is quite simple. What is Diversity? Consider the following two different cases. Many phenomena in the world need a series of outcomes to succeed. For instance, for life to exist in the cold and dark universe, we need a star to provide energy as heat. A planet is also required as a home. Furthermore, this planet must reside in the Goldilocks Zone of that

Continue reading
Spectral efficiency R_b/B versus E_b/N_0 determines the overall merit of a modulation scheme. This figure is drawn for BER = 10^{-5} and a Square-Root Raised Cosine pulse with 50% excess bandwidth
Wireless/SDR

Computing Error Rates

Having built a simple digital communication system, it is necessary to know how to measure its performance. As the names say, Symbol Error Rate (SER) and Bit Error Rate (BER) are the probabilities of receiving a symbol and bit in error, respectively. SER and BER can be approximated through simulating a complete digital communication system involving a large number of bits and comparing the ratio of symbols or bits received in error to the total number of bits. Hence, \begin{equation}\label{eqCommSystemSER} \text{SER} = \frac{\text{No. of symbols in error}}{\text{Total no. of transmitted symbols}} \end{equation} and \begin{equation}\label{eqCommSystemBER} \text{BER} = \frac{\text{No. of bits in

Continue reading