Tag: WiFi

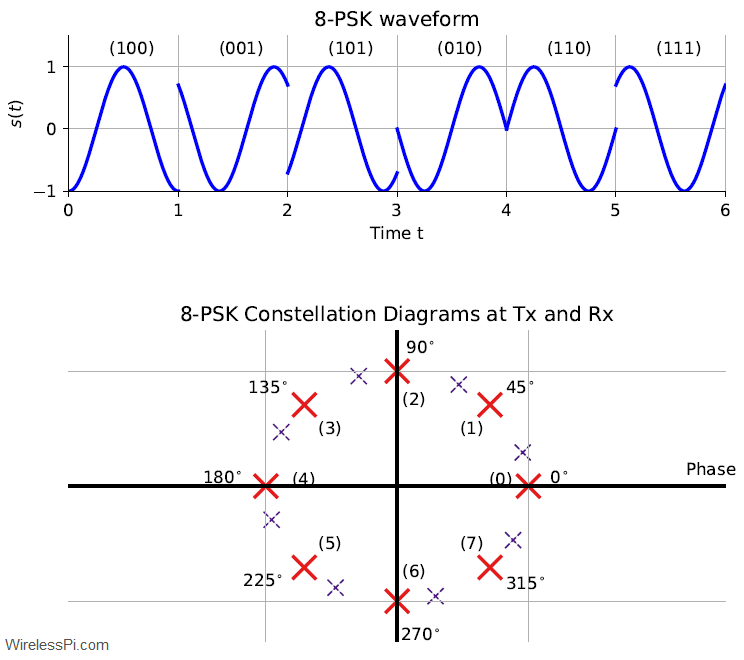
(Top) An 8-PSK waveform. (Bottom) Two constellation diagrams: one at the Tx shown by thick red lines and the other at the Rx for a phase offset of 17 degrees shown by dotted purple lines
DSP

I/Q Signals 101: Neither Complex Nor Complicated

Dec 04, 2020 There was a recent discussion on GNU Radio mailing list in regards to the simplest possible intuition behind I/Q signals. Why is I/Q sampling required? Question: The original question from Kristoff went like this: “… when you mention `GNU Radio complex numbers’, you also have to mention I/Q signals, which is a topic that is very difficult to explain in 10 seconds to an audience who has never seen anything about I/Q sampling before.” Comment: According to Jeff Long: “This is a great thing to try to figure out. If we can come up with an answer

Continue reading
A quasi-static assumption implies that the channel stays the same for each block but varies from one block to the next
Wireless/SDR

A Time-Varying Wireless Channel

Today we will discuss three strategies that are usually adopted for handling a wireless channel that is varying with time and hence acting differently on different data symbols. For a channel impulse response $c(t)$, number of multipath $N_{MP}$, channel gains $\gamma_i(t)$ and delays $\tau_i(t)$ for the $i$-th path, respectively, we can write \begin{equation*} c_B(t) = \sum _{i=0}^{N_{MP} -1} \gamma_i(t) \cdot \delta(t-\tau_i(t)) \end{equation*} i.e., channel gains $\gamma_i(t)$ and channel delays $\tau_i(t)$ are varying with time albeit at different rates. With the movement in the channel, the taps in a frequency selective channel are changing according to the rotation rates of path

Continue reading
A general QAM detector with respective waveforms at each block
Wireless/SDR

Quadrature Amplitude Modulation (QAM)

Quadrature Amplitude Modulation (QAM) is a spectrally efficient modulation scheme used in most of the high-speed wireless networks today. We discussed earlier that Pulse Amplitude Modulation (PAM) transmits information through amplitude scaling of the pulse $p(nT_S)$ according to the symbol value. To understand QAM, two routes need to be traversed. Route 1 We start the first route with differentiating between baseband and passband signals. A baseband signal has a spectral magnitude that is nonzero only for frequencies around origin ($F=0$) and negligible elsewhere. An example spectral plot for a PAM waveform is shown below for 500 2-PAM symbols shaped by

Continue reading