Articles | Page 24 of 35

August 15, 2022 DSP

Goertzel Algorithm – Evaluating DFT without DFT

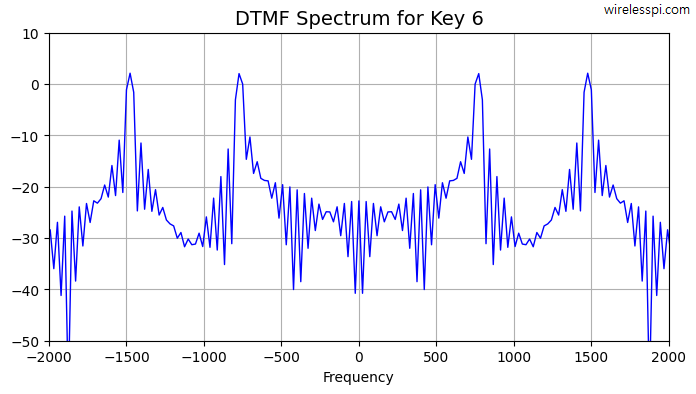
The Discrete Fourier Transform (DFT) computes the contribution of $N$ sinusoids that come together to form any input signal. However, in some applications, we are only interested in contributions from one or a few sinusoids This is where the Goertzel algorithm, proposed by Gerald Goertzel in 1958, comes in. The Goertzel algorithm evaluates the individual terms of the DFT in an efficient manner. We explain its derivation and implementation with the help of DTMF signals. DTMF Signal Generation In the early days of telephone, you could not call anyone directly. Instead, a telephone operator used to sit on the other

A digital signal and its underlying continuous waveform

February 27, 2022 Wireless/SDR

Why Digital Communication is Superior to Analog Communication

At the beginning, the history of wireless communication revolved around analog communication systems for several decades. Amplitude Modulation (AM) and Frequency Modulation (FM) were the most widely used techniques during this time. Gradually, however, a transition towards digital transmission occurred in wireless systems as well, a phenomenon that was in sync with digital revolution in the society as a whole. So what are the main benefits of digital technology that made it much superior to its analog counterpart? Let us analyze some of them below [1]. Performance Analog signals suffer from distortion and noise, even if they are small. Although

Width of a sinc signal increases and approaches a constant, just like an eagle spreading its wings

November 7, 2016 DSP

A Unit Impulse in Continuous-Time

This post treats the signals in continuous time which is different than the approach I adopted in my book which deals exclusively in discrete time. A unit impulse is defined as \begin{equation*} \delta (t) = \displaystyle{\lim_{\Delta \to 0}} \begin{cases} \frac{1}{\Delta} & -\frac{\Delta}{2} < t < +\frac{\Delta}{2} \\ 0 & \text{elsewhere} \end{cases} \end{equation*} The result is an impulse with zero width and infinite height, but a consequence of defining it in this way is that the area under the curve is unity. \begin{equation*} \text{Area under a rectangle} = \Delta \cdot \frac{1}{\Delta} = 1 \end{equation*} This is shown in Figure below. Stated

Eye diagrams for I arm of a 4-QAM signal for 15, 30 and 45 degrees phase offsets and a Raised Cosine filter with excess bandwidth 0.5. A similar eye diagram exists for Q arm as well

December 23, 2016 Wireless/SDR

What is Carrier Phase Offset and How It Affects the Symbol Detection

In case of Quadrature Amplitude Modulation (QAM) and other passband modulation schemes, Rx has no information about carrier phase of the Tx oscillator. Let us explore what impact this has on the demodulation process. Constellation Rotation To see the effect of the carrier phase offset, consider that a transmitted passband signal consists of two PAM waveforms in $I$ and $Q$ arms denoted by $v_I(t)$ and $v_Q(t)$ respectively and combined as \begin{equation}\label{eqRealWorldQAMPhaseOffset} s(t) = v_I(t) \sqrt{2} \cos 2\pi F_C t – v_Q(t) \sqrt{2}\sin 2\pi F_C t \end{equation} Here, $F_C$ is the carrier frequency and $v_I(t)$ and $v_Q(t)$ are the continuous versions

For the same area and their spacing (with respect to the wavelength), the number of elements in the array at high band is larger thus capturing a similar or increased amount of power

December 20, 2021 Wireless/SDR

Free Space Propagation in mmWave Systems

In this article, we describe the free space propagation in mmWave systems. During the discussion, we dispel a common myth that the received power at any distance decays with increasing carrier frequency. We will see that the received power is in fact independent of the carrier frequency for suitably designed systems such as those at mmWave frequencies. Instead, it is only after including the atmospheric effects such as water vapors, oxygen, rain and penetration loss in materials that the carrier frequency plays a substantial role in establishing the link budget. Suppose that a Tx transmits $P_{\text{Tx}}$ watts of power uniformly