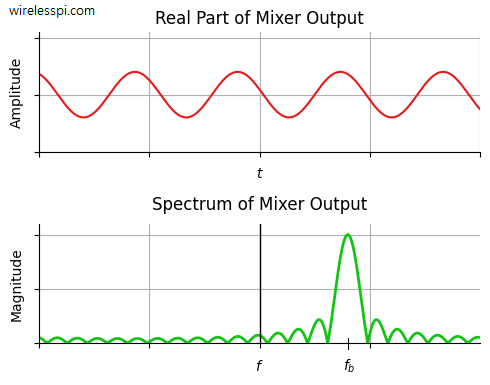
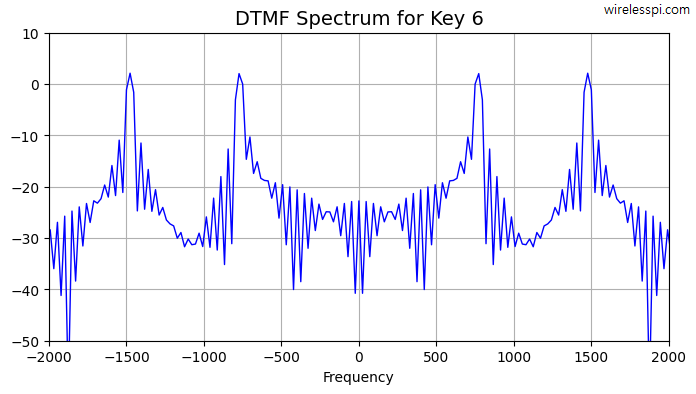
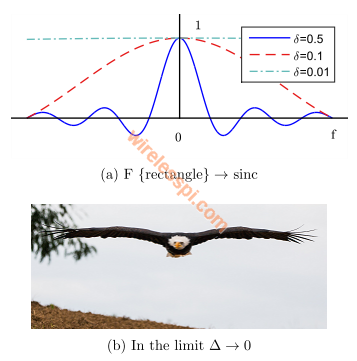
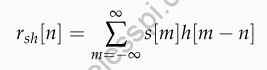Category: DSP

Digital Signal Processing

Square-root Nyquist filters for three different excess bandwidths
DSP / Wireless and SDR

How to Design Nyquist and Square-Root Nyquist Pulse Shaping Filters

The radio spectrum is a very precious resource like real estate and must be utilized judiciously. Pulse shaping filters control the spectral leakage of the transmitted signal in a wireless channel due to the strict restrictions to comply with a spectral mask. This is even more important for the upcoming 5G wireless systems which are based on a variety of wireless transmission protocols (such as mobile networks, Internet of Things (IoT) and machine to machine communications) combined in one comprehensive standard. Even for wired channels, there is always a natural bandwidth of the medium (copper wire, coaxial cable, optical fiber)

Continue reading
A discrete-time integrator implemented through a forward difference and a backward difference technique
DSP

Discrete-Time Integrators

An integrator is a very important filter that proves useful in implementation of many blocks of a communication receiver such as symbol timing synchronization and Phase-Locked Loop (PLL). It is an inverse operation to a differentiator that is also used in many signal processing applications such as FM demodulation and image processing. In continuous-time case, an integrator finds the area under the curve of a signal amplitude. A discrete-time system deals with just the signal samples and hence a discrete-time integrator serves the purpose of collecting a running sum of past samples for an input signal. Looking at an infinitesimally

Continue reading
Frequency response of a moving average filter
DSP

Moving Average Filter

The most commonly used filter in DSP applications is a moving average filter. In today’s world with extremely fast clock speeds of the microprocessors, it seems strange that an application would require simple operations. But that is exactly the case with most applications in embedded systems that run on limited battery power and consequently host small microcontrollers. For noise reduction, it can be implemented with a few adders and delay elements. For lowpass filtering, an excellent frequency domain response and substantial suppression of stopband sidelobes are less important than having a basic filtering functionality, which is where a moving average

Continue reading
Beat frequency sinusoid and its spectrum
DSP

Spectrum of a Sinusoid

In this article, we derive the spectrum of a complex sinusoid that acts as the basis for all spectra. In fact, the very definition of the Fourier Transform, whether continuous or discrete, comes from the perspective of a complex sinusoid. Therefore, exploring this derivation will be useful in everything else we learn about DSP. For an in-depth understanding of complex signals and I/Q processing, you can read the following two articles (the option of downloading them as PDF is available). The origin of complex numbers and signals I/Q signal processing from the ground up Let us start with the continuous-time

Continue reading
Definition of correlation
DSP / Machine Learning

The Master Algorithm

Recently, I was reading the book The Master Algorithm by Pedro Domingos — a Professor at the University of Washington in machine learning. According to the description of his book, The Master Algorithm in Machine Learning A spell-binding quest for the one algorithm capable of deriving all knowledge from data, including a cure for cancer. Society is changing, one learning algorithm at a time, from search engines to online dating, personalized medicine to predicting the stock market. But learning algorithms are not just about Big Data – these algorithms take raw data and make it useful by creating more algorithms.

Continue reading