DSP Archives | Page 11 of 15

August 26, 2016 DSP

The Concept of Frequency

A wireless signal from one device to another travels through the use of electromagnetic waves propagated by an antenna. Electromagnetic waves have different frequencies and one can pick up a specific signal by tuning a radio Rx to a specific frequency. But what is a frequency anyway? Watch the video below for an interesting description of actual time domain samples and how to interpret their frequency domain representation. A Complex Sinusoid Consider a complex number $V$ in an $IQ$-plane. A complex number is defined as a pair of real numbers in $(x,y)$-plane similar to the vectors but with different arithmetic

All symbol intervals are overlayed on top of one another and the time axis is shifted to bring ideal sampling instant in the middle. Eye diagram generated for 250 2-PAM symbols and Square-Root Raised Cosine pulse with excess bandwidth 0.5

August 21, 2016 DSP

Tools for Signal Diagnosis

In this article, we will devise some tools that help us diagnose problems with the communication system under study. I like to call them the stethoscopes for a communication system due to the crucial functionality they provide regarding the health of the communication system being analyzed. We discuss three such tools, namely an eye diagram, a transition diagram and a scatter plot below. Eye Diagram An eye diagram is an excellent summary of the signal behaviour in time domain, something analogous to a spectrum in frequency domain. Imagine the samples of the matched filter output taken at a much higher

August 13, 2026 DSP

Derivations of 3-dB and Loop Noise Bandwidths

Loop bandwidth is the most important parameter in a Phase Locked Loop (PLL) for phase synchronization and PLL for timing recovery. Today we will cover its significance and derive the relevant expressions. Loop Bandwidth Loop bandwidth is the frequency range over which a PLL can effectively track variations in the phase and frequency of its input reference signal. It not only serves as the primary filtering metric for the system but also determines how quickly the PLL can lock into convergence. As with most other technical concepts, the loop bandwidth presents a critical design trade-off: the smaller the loop bandwidth,

August 18, 2016 DSP

Discrete Frequency

An Analog to Digital Converter (ADC) samples a continuous-time signal to produce discrete-time samples. For a digital signal processor, this signal just resides in memory as a sequence of numbers. Consequently, the knowledge of the sample rate $F_S$ is the key to signal manipulation in digital domain. As far as time is concerned, one can easily determine the period or frequency of such a signal stored in the memory. For example, the period $T$ in the sinusoid of Figure below is clearly $10$ samples and sample time $T_S=1/F_S$ can be employed to find its period in seconds. For a sample

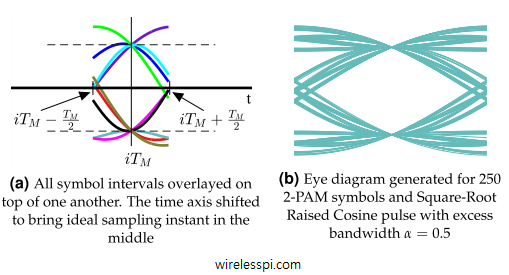
Magnitude of frequency response |H[k]| in response to complex sinusoids at all N frequencies

August 12, 2016 DSP

System Characterization

In wireless communications and other applications of digital signal processing, we often want to modify a generated or acquired signal. A device or algorithm that performs some prescribed operations on an input signal to generate an output signal is called a system. In another article about transforming a signal, we saw how a signal can be scaled and time shifted, or added and multiplied with another signal. These are all examples of a system. Amplifiers in communication receivers and filters in image processing applications are some systems that we interact with in daily lives. A communication channel is also a