DSP Archives | Page 12 of 15

August 13, 2016 DSP

Transforming a Signal

Transforming a discrete-time signal — whether in time or amplitude — is certainly possible, and often in interesting ways. In practice, scaling and time shifting are the two most important signal modifications encountered. Scaling changes the values of dependent variable on amplitude-axis while time shifting affects the values of independent variable on time-axis. Below we describe addition and multiplication of two signals as well as scaling and time shifting a signal in detail. Addition For addition of two discrete-time signals, say $x[n]$ and $y[n]$, add the two signals sample-by-sample: $z[n] = x[n] + y[n]$ for every $n$, e.g., \begin{align*} z[0]

Magnitude and phase of the DFT of a rectangular signal for L = 7, N= 16 and starting sample shifted by one

August 12, 2016 DSP

DFT Examples

For understanding what follows, we need to refer to the Discrete Fourier Transform (DFT) and the effect of time shift in frequency domain first. Here, we discuss a few examples of DFTs of some basic signals that will help not only understand the Fourier transform but will also be useful in comprehending concepts discussed further. A Rectangular Signal A rectangular sequence, both in time and frequency domains, is by far the most important signal encountered in digital signal processing. One of the reasons is that any signal with a finite duration, say $T$ seconds, in time domain (that all practical

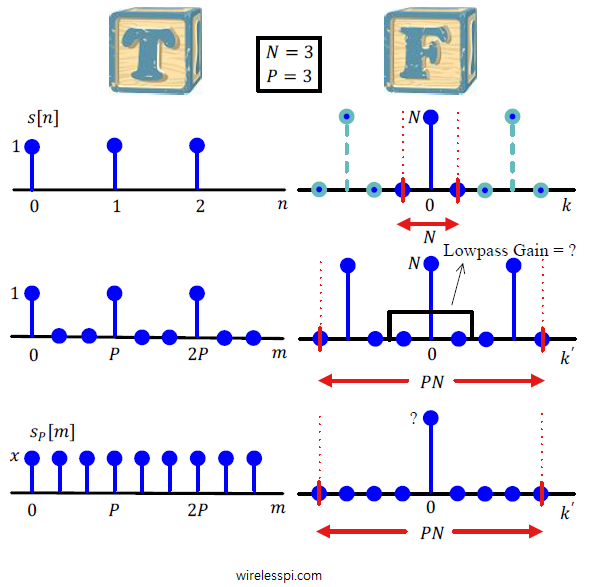
A rectangular signal and its upsampled version in time and frequency domains

August 3, 2016 DSP

Sample Rate Conversion

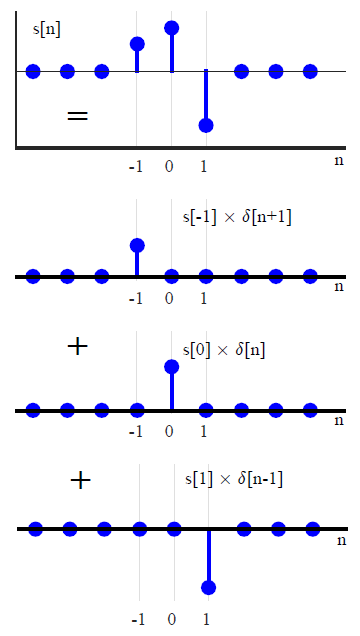
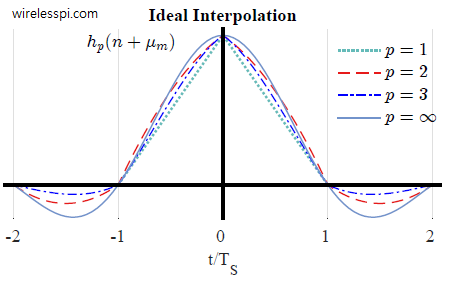
In the discussion on sampling, the process of sampling a continuous-time signal was discussed in detail and subsequently sampling theorem was derived. In many applications, resampling an already digitized signal is mandatory for an efficient system design. In wireless communications, sample rate conversion is utilized for upconversion and downconversion to a desired frequency, filtering stages in the digital frontend and sometimes for carrier and timing synchronization during signal acquisition. See the Cascade Integrator Comb (CIC) filters for how to accomplish this task with minimal resources. In discrete domain, sample rate can be reduced by discarding intermediate samples periodically called downsampling

A signal broken down into scaled and shifted impulses

August 9, 2016 DSP

Convolution

Understanding convolution is the biggest test DSP learners face. After knowing about what a system is, its types and its impulse response, one wonders if there is any method through which an output signal of a system can be determined for a given input signal. Convolution is the answer to that question, provided that the system is linear and time-invariant (LTI). We start with real signals and LTI systems with real impulse responses. The case of complex signals and systems will be discussed later. Convolution of Real Signals Assume that we have an arbitrary signal $s[n]$. Then, $s[n]$ can be

August 2, 2016 DSP

The Discrete Fourier Transform (DFT)

Learned in some other articles on this website, the following three important concepts take us to the core of the Discrete Fourier Transform (DFT) idea. Regardless of the signal shape, most signals of practical interest can be considered as a sum of complex sinusoids oscillating at different frequencies. A set of $N$ orthogonal complex sinusoids can be constructed within a span of $N$ time domain samples. Each `tick’ or bin on the discrete frequency axis denotes the discrete frequency $k/N$ of such a complex sinusoid. To understand how a set of sinusoids with $N$ discrete frequencies can sum up to