Tag: Quadrature Amplitude Modulation (QAM)

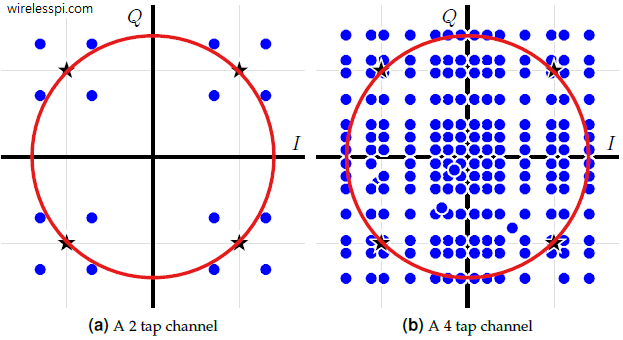
Scatter plot for a QPSK signal after filtering through a channel
Wireless/SDR

An Introduction to Constant Modulus Algorithm (CMA)

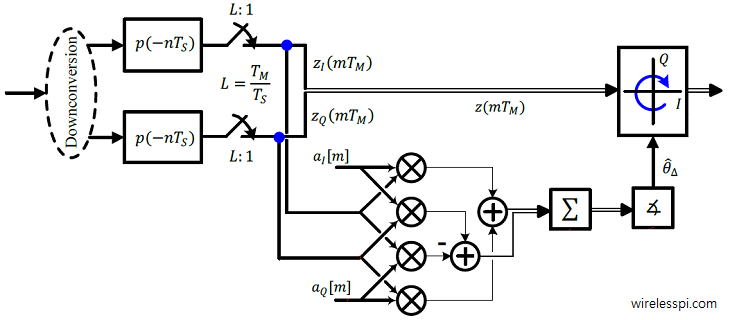
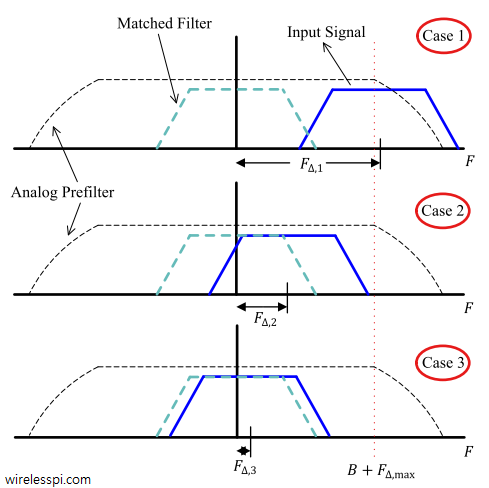
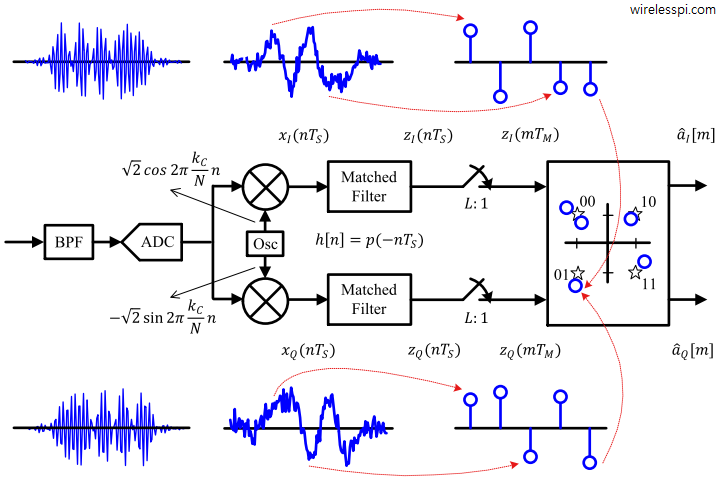
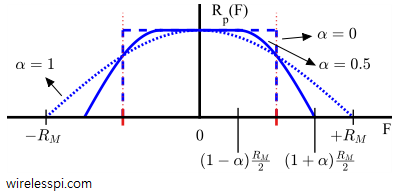
In many kinds of equalizers such as maximum likelihood sequence estimation, the channel response is available at the Rx through any channel estimation procedure that requires a training sequence. For adaptive equalization such as Least Mean Square (LMS) equalizers or Decision Feedback Equalization (DFE), first the training sequence symbols and then symbol decisions are employed to tune the equalizer taps. There are many applications, however, where the Rx needs to acquire the equalizer coefficients without any help from the Tx in the form of known symbols. This is a non-data-aided scenario that is primarily required in mobile communication systems where

Continue reading
A block diagram for the implementation of the feedforward phase estimator
Wireless/SDR

How to Estimate the Carrier Phase

In this article, I will describe how to estimate the carrier phase from an incoming waveform in a feedforward manner. This algorithm utilizes a sequence of known pilot symbols embedded within the signal along with the unknown data symbols. Such a signal is sent over a link in the form of separate packets in burst mode wireless communications. In most such applications with short packets, the phase offset $\theta_\Delta$ remains constant throughout the duration of the packet and a single shot estimator is enough for its compensation. Here, the primary task of the designer is to develop this closed-form expression

Continue reading
Three different cases for carrier frequency offset
Wireless/SDR

What is Carrier Frequency Offset (CFO) and How It Distorts the Rx Symbols

In Physics, frequency in units of Hz is defined as the number of cycles per unit time. Angular frequency is the rate of change of phase of a sinusoidal waveform with units of radians/second. \begin{equation*} 2\pi f = \frac{\Delta \theta}{\Delta t} \end{equation*} where $\Delta\theta$ and $\Delta t$ are the changes in phase and time, respectively. A Carrier Frequency Offset (CFO) usually arises due to two reasons. The video below also explains this concept. [Frequency mismatch between the Tx and Rx oscillators] No two devices are the same and there is always some difference between the manufacturer’s nominal specification and the

Continue reading
A general QAM detector with respective waveforms at each block
Wireless/SDR

Quadrature Amplitude Modulation (QAM)

Quadrature Amplitude Modulation (QAM) is a spectrally efficient modulation scheme used in most of the high-speed wireless networks today. We discussed earlier that Pulse Amplitude Modulation (PAM) transmits information through amplitude scaling of the pulse $p(nT_S)$ according to the symbol value. To understand QAM, two routes need to be traversed. Route 1 We start the first route with differentiating between baseband and passband signals. A baseband signal has a spectral magnitude that is nonzero only for frequencies around origin ($F=0$) and negligible elsewhere. An example spectral plot for a PAM waveform is shown below for 500 2-PAM symbols shaped by

Continue reading
Square-Root Raised Cosine (SR-RC) spectrum with different excess bandwidths
Wireless/SDR

Modulation Bandwidths

From the article on pulse shaping, we can correctly determine the occupied bandwidth for each modulation scheme where the Square-Root Raised Cosine spectrum shows the bandwidth of a Square-Root Raised Cosine pulse shape as $0.5(1+\alpha)R_M$. Also, we have discussed earlier that the spectrum approximately remains the same, provided that there is enough randomness in bit stream and the resulting symbols are equally likely and independent from each other. Therefore, the bandwidth for a PAM modulated signal can be given as \begin{equation}\label{eqCommSystemBWPAM} BW_{\text{PAM}} = 0.5\left(1+\alpha\right)R_M \end{equation} QAM is basically a similar modulation scheme except that it is modulated on a carrier.

Continue reading