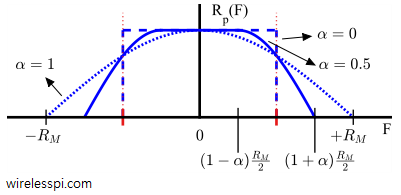
From the article on pulse shaping, we can correctly determine the occupied bandwidth for each modulation scheme where the Square-Root Raised Cosine spectrum shows the bandwidth of a Square-Root Raised Cosine pulse shape as $0.5(1+\alpha)R_M$. Also, we have discussed earlier that the spectrum approximately remains the same, provided that there is enough randomness in bit stream and the resulting symbols are equally likely and independent from each other. Therefore, the bandwidth for a PAM modulated signal can be given as
BW_{\text{PAM}} = 0.5\left(1+\alpha\right)R_M
\end{equation}
QAM is basically a similar modulation scheme except that it is modulated on a carrier. After the spectral upconversion, both positive and negative portions of the baseband spectrum appear at $+F_C$ and $-F_C$. The bandwidth — positive portion of the spectrum — hence becomes double.
BW_{\text{QAM}} = 2(0.5)\left(1+\alpha\right)R_M = (1+\alpha)R_M
\end{equation}
The same equation holds for PSK modulation. In case some other pulse shape is used with a bandwidth $B$, the factor $0.5(1+\alpha)$ can be replaced with $B$ in the above equations.