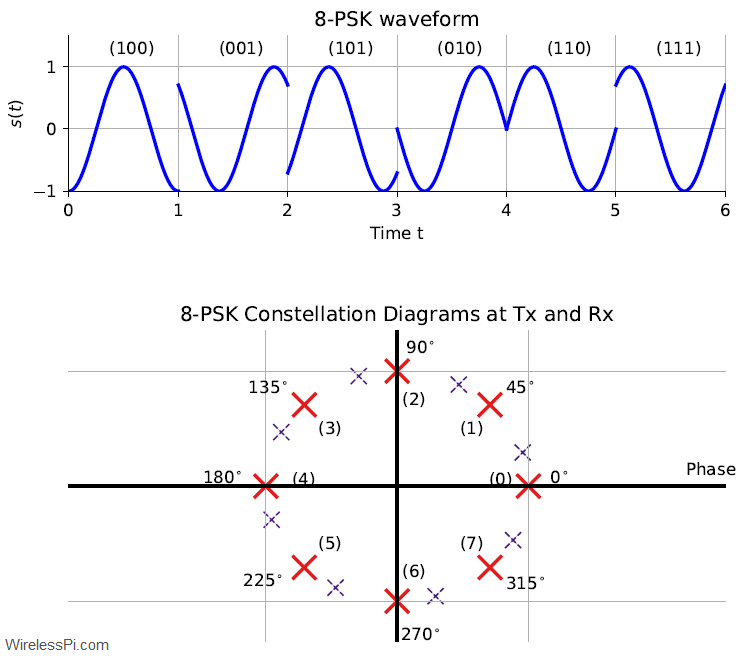
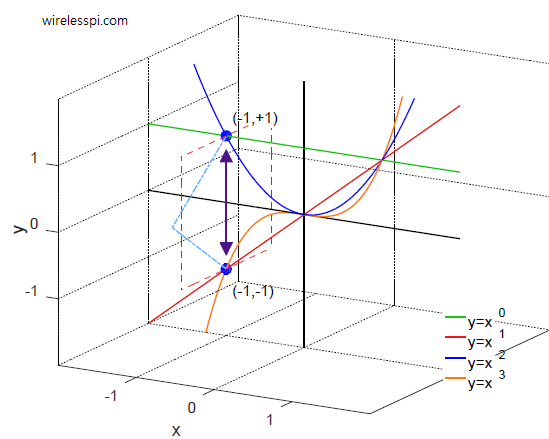
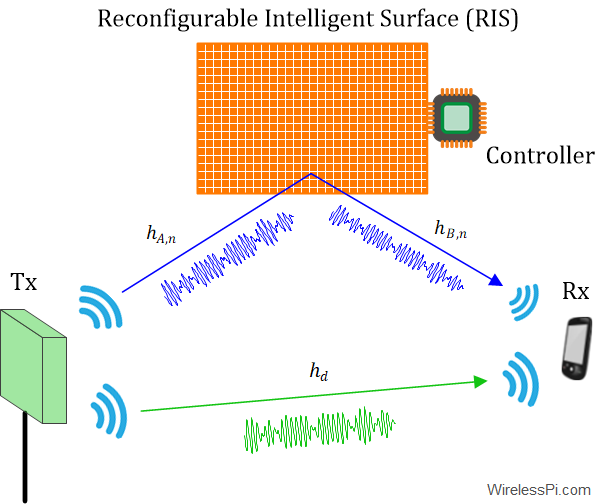
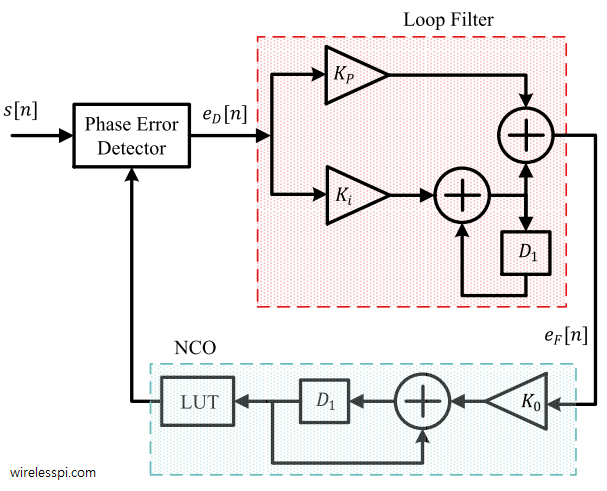
One of the most memorable phrases in television history is the command from Captain Kirk to his chief engineer Scotty in the science fiction series Star Trek:
“Beam me up, Scotty!”
It refers to the futuristic teleportation machine, known as a Transporter, which disassembles a person or object into an energy pattern, then beam it to a target site where it is reassembled into the original matter.

From Mechanics to Energy Beams
Imagine that such a device is invented at a point in the future. Until then, the knowledge of a person relating to transportation through automobiles is based on an internal combustion engine, pistons, crankshaft and so on. Suddenly we find ourselves in a completely different territory because designing and building the technology for transporting a person from location A to location B is now based around mass-energy equivalence in physics, according to which mass and energy are the same physical entity and can be converted into each other. Not only do we need to understand
\begin{equation*}
E=mc^2
\end{equation*}
from Albert Einstein’s theory of special relativity but also come up with optimal strategies to reproduce as closely as possible the said person or object from the incoming beam. This is a process that requires excellent mental models of the underlying mass $\leftrightarrow$ energy conversion phenomena, not the mechanics of the engine.

From Electronics to DSP
In not as dramatic but still a similar manner, wireless communications has profoundly transformed as a science in the previous years due to the digital revolution.
- On the transmitter side, we have become able to send into air a sequence of numbers stored in a processor memory.
- On the receiver side, we have become able to acquire the momentary value of the incoming analog signal and convert it into its digital representation which is nothing but a sequence of numbers, known as a discrete-time sequence.
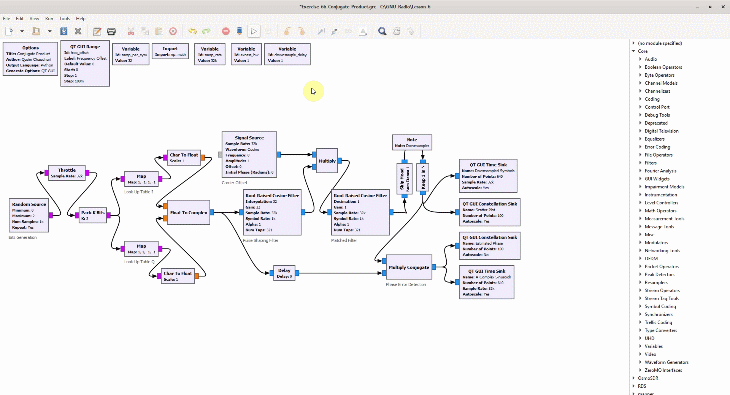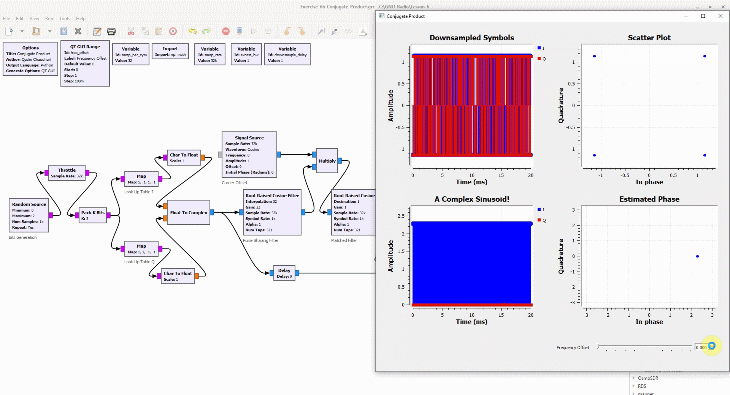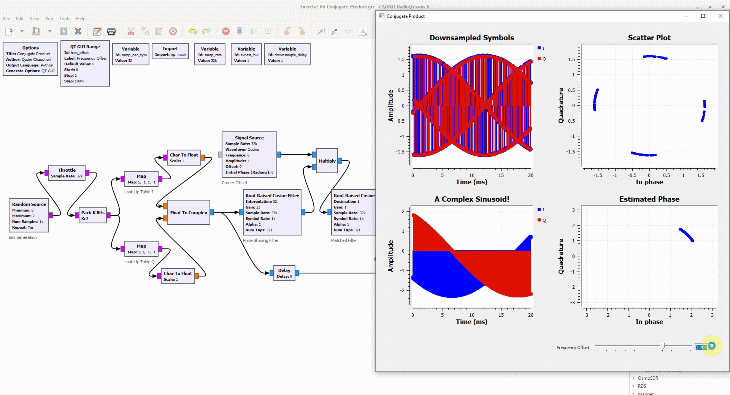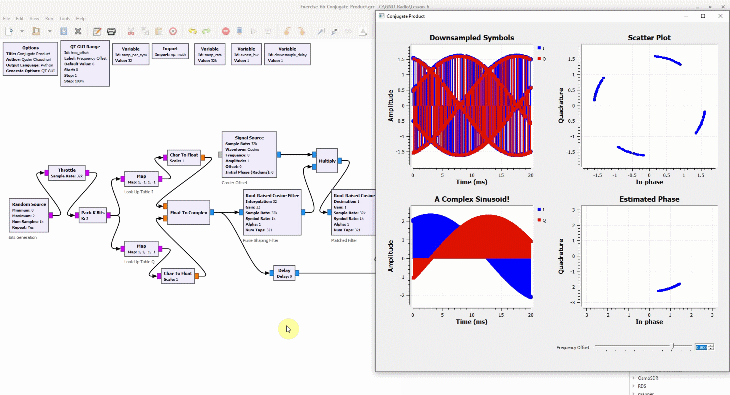
After the great advancement in computational power, most of the radio circuits capable of performing analog signal processing (e.g., by using resistors, capacitors, inductors, op amps — basically physics and devices) have been replaced by powerful digital processors that can perform the necessary number crunching (basically algorithms run by computer programs) to unravel the original digital information. In a true software radio, this is a process that requires excellent mental models of the underlying discrete-time sequences, not the electronics of the circuits.
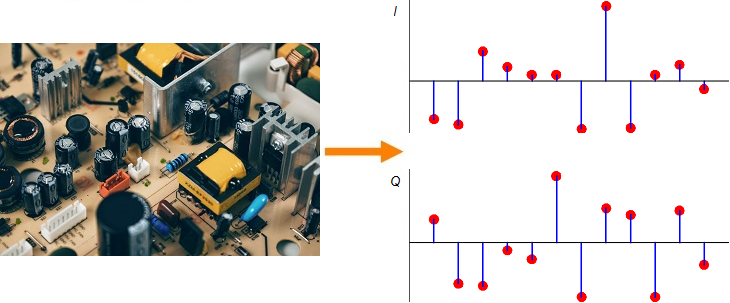
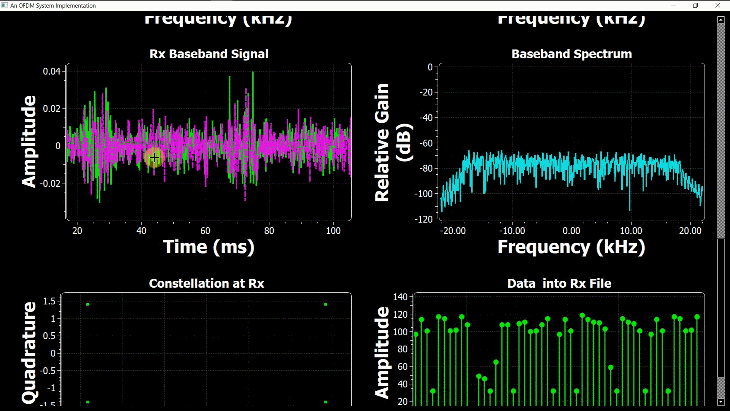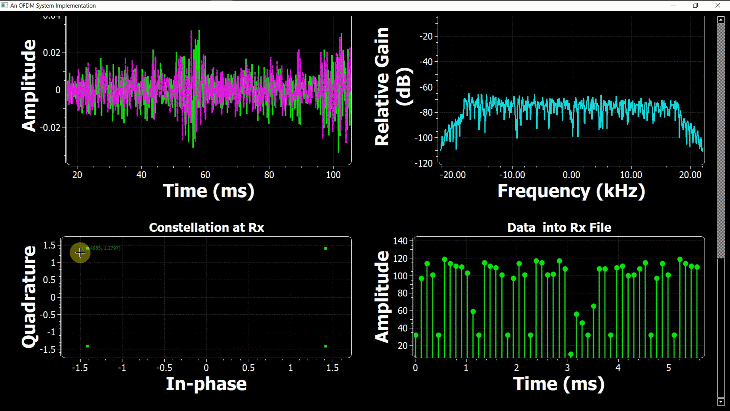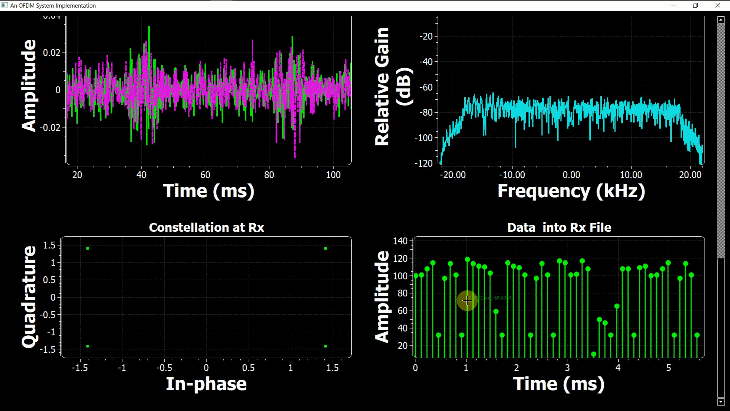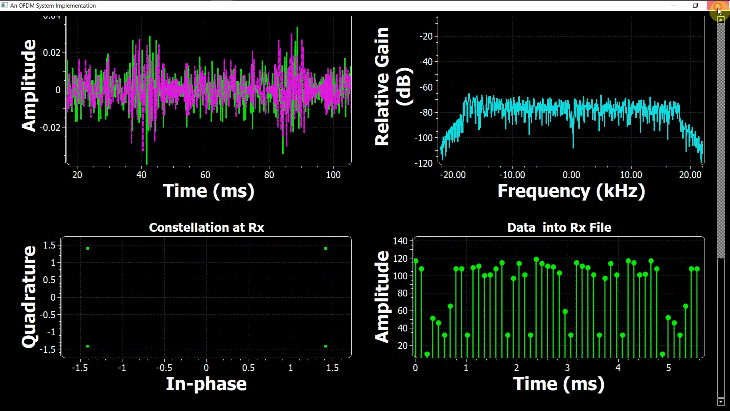
Shown on the right side above is a discrete-time sequence that consists of a few random bits 0s and 1s mapped to signal levels -1s and +1s, respectively. Why does it look more complicated than a stream of -1s and +1s? Because in the real world, this signal has been distorted by the following impairments before presenting itself to the Rx processing machine.
- Carrier phase offset: 17˚
- Timing phase offset: 31% of a bit time
- Carrier frequency offset: 11% of the bit rate
- Multipath channel: A direct path and two reflected paths with relative amplitudes of 0.6 and 0.2 arriving after relative delays of 0.76 and 1.03, respectively
(If you are unfamiliar with the above terms, there is no need to worry. This website has plenty of explanations on these topics.) The I and Q parts shown in the above figure are the two components of a complex signal. I cover complex numbers as a starting point to build our Digital Signal Processing (DSP) toolkit. Also, I like to view the same IQ signal in a 3D figure as shown below which offers several advantages over the separate two 2D figures.
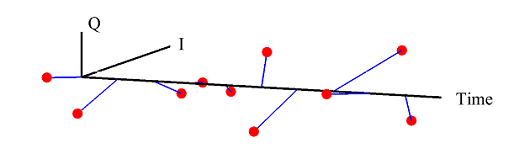
By just looking at the above figure, it is hard to believe that extracting the original stream of bits 0s and 1s from this complex sequence is even possible after so much distortion. Nevertheless, this amazing (ad)venture can be accomplished through implementation of DSP algorithms in a programming language such as Python or Matlab. This is all a Software Defined Radio (SDR) is about, see the figure below.
Why Wireless Pi?
My name is Qasim Chaudhari and I write about software defined radio and wireless communications in a different style as compared to several other wonderful resources available on these topics.
- As you will find in the introduction of my book, any language, including that of mathematics, is an unnatural mode of communication. On the other hand, showing an image makes almost every single person on the planet immediately get the concept. A figure imprints a massive amount of parallel information in our brains that is much easier to process and recall later. Since a human mind handles images very well, I make the reader visualize the equations through beautiful figures.
- I only rely on school level mathematics to explain all the concepts. The only things to know are a sine, cosine and a summation as well as (occasionally) a derivative.
- Almost everything I have written has been built from the ground up and intuitive explanations are presented behind the ideas.
In the past when only humans could read, we wrote scientific material in a machine-like manner. Now when the machines are learning to read, why not turn towards a more human-like style. In my opinion, there is no harm in writing technical stuff with a human touch, see some examples below.
Popular Articles
Join Me
My work is read by a diverse range of people around the world. You can join my monthly newsletter through entering your email below.