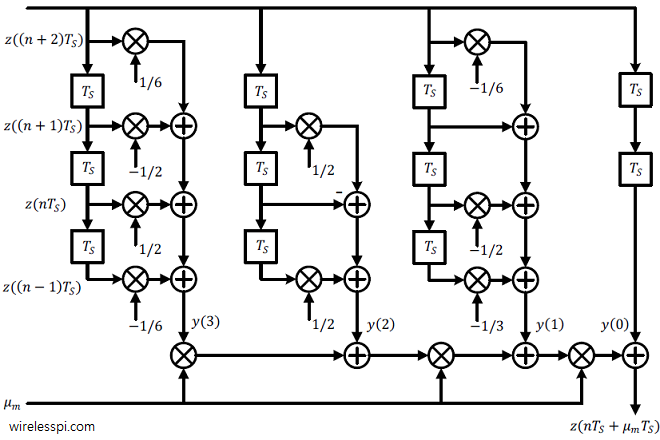
Farrow structure for cubic interpolation
DSP

Fractional Delay Filters Using the Farrow Structure

In the discussion on piecewise polynomial interpolation, we emphasized on the fact that the fractional interval $\mu_m$ needs to be updated for each symbol time $mT_M$ and hence the subscript $m$ in $\mu_m$. For this reason, the interpolation process becomes a two-step procedure. Update the filter coefficients $h_p[n]$. Perform the convolution between $z(nT_S)$ and $h_p[n]$. This process can be simplified if the two steps above can be combined in such a way that $\mu_m$ update is weaved into the convolution operation. In other words, instead of a two-input hardware multiplication with two variable quantities, complexity can be reduced by restructuring

Continue reading
A beam formation process can be seen in water waves by throwing two stones
Localization / Wireless/SDR

Beamforming – Mindfulness of an Antenna Array

If beamforming has to be explained in the most succinct manner, it is the mindfulness of an antenna array where it focuses its attention towards one specific location (or a few specific locations). We find out in this article how it is achieved. As opposed to its reputation, beamforming is not a mysterious technology. It has been used by signal processing engineers for radio applications since long. For example, Marconi used four antennas to increase the gain of signal transmissions across the Atlantic in 1901. It has also been known since 1970s that multiple antennas at the base station help

Continue reading
Symbolic representation of linear phase rotation that changes with frequency index
DSP

Effect of Time Shift in Frequency Domain

Children usually ask questions like “How many hours have passed?” And they have no idea about the start time to be taken as a reference. Just like the zero of a measuring tape, a zero reference for time plays a crucial role in analyzing the signal behaviour in time and frequency domains. Until now, we assumed that reference time $0$ coincides with the start of a sine and a cosine wave to understand the frequency domain. Later, we will deal with symbol timing synchronization problem in single-carrier systems and carrier frequency synchronization problem in multicarrier systems, both of which address

Continue reading
Classification of carrier frequency synchronization algorithms
Wireless/SDR

Classification of Carrier Frequency Synchronization Techniques

We have discussed before that carrier phase synchronization is done at the end of the Rx signal processing chain due to the very nature of the DSP implementation. And that almost all DSP based phase synchronization algorithms are timing-aided. Timing acquisition implies knowing the symbol boundaries in the Rx sampled waveform which is equivalent to identifying the optimal sampling instants where the eye opening is maximum and Inter-Symbol Interference (ISI) from the neighbouring symbols is zero. In the case of Carrier Frequency Synchronization (CFO), this is not true. From a previous post on the effect of CFO, we know that

Continue reading
SINAD for signal, noise and distortion
Wireless/SDR

How to Compute SINAD in a Radio Receiver

In theory, the quantity that determines the performance of a radio receiver is the Signal to Noise Ratio (SNR). In linear terms, this is simply the ratio of the signal power versus the noise power appearing at the demodulator input. \[ SNR = 10\log_{10} \frac{P_S}{P_N} \] where $P_S$ is the signal power and $P_N$ is the noise power within the spectrum. However, when experimental measurements are carried out in order to verify the theoretical conclusions, SNR alone is not enough and there is another quantity, known as SINAD, that governs the receiver performance. What is SINAD SINAD stands for Signal

Continue reading