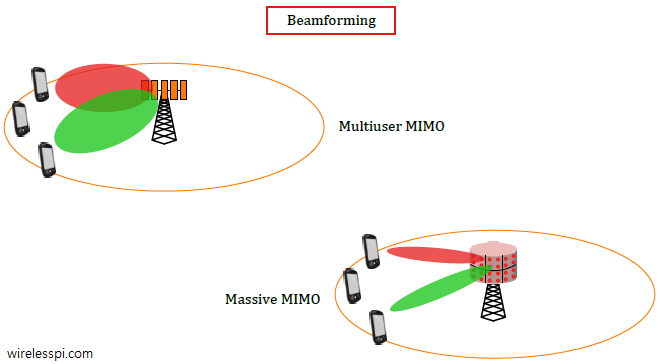
Beamforming in multi-user vs massive MIMO systems
Wireless/SDR

Zero-Forcing (ZF) Detection in Massive MIMO Systems

Massive MIMO is one of the defining technologies in 5G cellular systems. In a previous article, we have described spatial matched filtering (or maximum ratio) as the simplest algorithm for signal detection. Here, we explain another linear technique, known as Zero-Forcing (ZF), for this purpose. It was described before in the context of simple MIMO systems here. Background Consider the block diagram for uplink of a massive MIMO system as drawn below with $N_B$ base station antennas and $K$ mobiler terminals. It is evident that the cumulative signal at each base station antenna $j$ is a summation of signals arriving

Continue reading
DSP / Wireless/SDR

Antenna Arrays: Whole is More than its Parts

In a previous article, we described how multiples antennas can be viewed as sampling the signal in space domain in a direct analogy to sampling the signal in time domain. Filters in discrete-time domain are usually defined by numerical values in the time axis. Space allows three-dimensional freedom. A filter in discrete space can have its elements placed anywhere in the space. This sounds very complicated! But we will show it is not. A Simple Time Domain Filter: 2-Tap FIR The simplest discrete FIR filter has only two samples of unit magnitude. Assuming unit magnitude and zero phase for both

Continue reading
A timing locked loop with a Gardner TED converging to the steady state value for a square-root raised cosine pulse with excess bandwidth 0.4
Wireless/SDR

Gardner Timing Error Detector: A Non-Data-Aided Version of Zero-Crossing Timing Error Detectors

Timing synchronization plays the role of the heart of a digital communication system. We have already seen how a timing locked loop, commonly known as symbol timing PLL, works where I explained the intuition behind the maximum likelihood Timing Error Detector (TED). A simplified version of maximum likelihood TED, known as Early-Late Timing Error Detector, was also covered before. Today we discuss a different timing synchronization philosophy that is based on zero-crossing principle. It is commonly known as Gardner timing recovery. Background Before we start this topic, I recommend that you read about Pulse Amplitude Modulation (PAM) for an introduction

Continue reading
Buridan's donkey at an equal distance from hay and water
Machine Learning

k-Nearest Neighbors (k-NN) – A Man is Known by the Company He Keeps

Aesop was a Greek storyteller who created lots of short stories more than 2500 years ago (such as the hare and the tortoise), now collectively known as Aesop’s Fables. "A man is known by the company he keeps" is a quote also attributed to him that has survived through the ages and has proven to be a timeless truth. The k-Nearest Neighbors (k-NN) algorithm is essentially based on the same idea. It suggests that when a machine needs to classify a new data point in an application, examining its neighboring data points is an effective strategy. In the spirit of

Continue reading
Projections of a sphere in Flatland
DSP / Wireless/SDR

Two Birds with One Tone: I/Q Signals and Fourier Transform – Part 2

In Part 1 of I/Q signals series, we saw the implications of orthogonality in amplitude and phase. Now we talk about orthogonality in frequency and see its implications in signal processing applications. Let us start with a new perspective that will resolve the 2nd mystery of I/Q signals. A Basic Building Block Humans use the power of logic to uncover the rules according to which the world works. But our minds struggle to retain excessive amounts of information required to grasp the complex reality. Therefore, we like to reduce everything around us as a combination of some fundamental unit, a

Continue reading