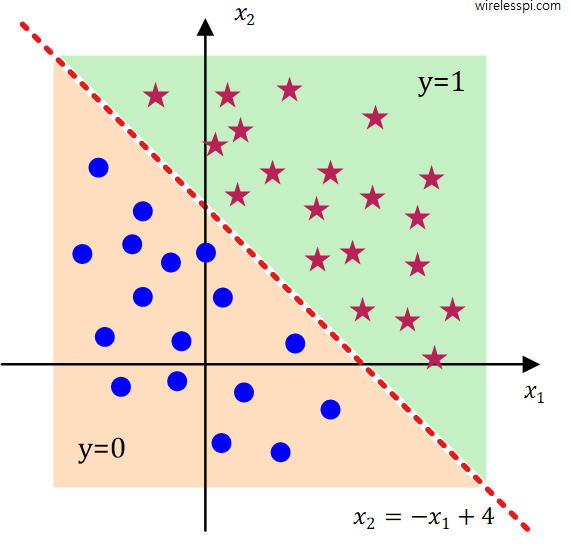
Decision boundary for multivariate logistic regression
Machine Learning

Logistic Regression in Machine Learning

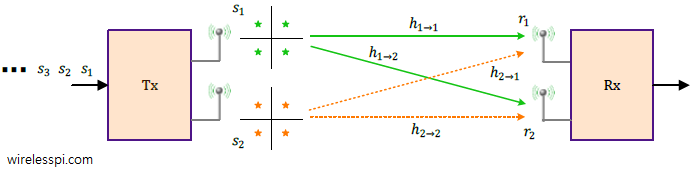
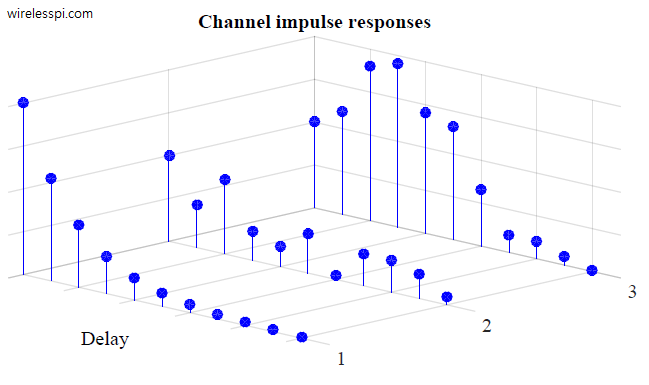
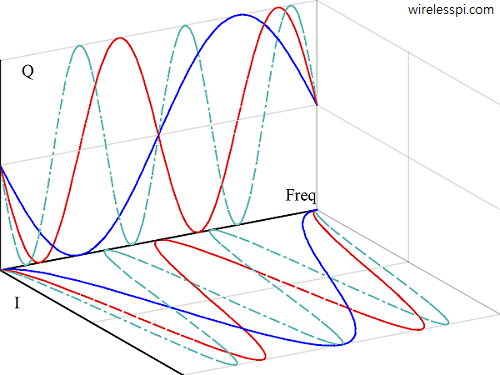
A hundred thousand years ago, our ancestors used to roam in the savannas and jungles. It was absolutely necessary for them to judge (or classify) everything they encounter: a movement in the bushes could be due to a harmless rabbit or a dangerous tiger, a fruit on a plant could be nutritious or poisonous, and so on. Then came the wizards who invented language and then people developed agriculture, writing and industry. The advancement in civilization and the quest for scientific knowledge revealed the benefits of a wide spectrum and viewing shades of gray instead of of simple black and

Continue reading
A 2x2 MIMO spatial multiplexing system
Wireless/SDR

Linear Detection Algorithms in MIMO Systems

In the past 100 years, scientists have imagined new ways of boosting the capacity of wireless channels. Around the middle of 20th century, we began to truly understand the role of fundamental players in this equation, namely power and bandwidth. It was realized that the capacity of a wireless channel increases logarithmically with SNR and hence quickly approaches the region of diminishing returns. Nevertheless, with a few exceptions, almost all the research was exclusively focused on single antenna systems. It was only in mid 1990s that the power of using multiple antennas at both ends of the link was discovered.

Continue reading
A quasi-static assumption implies that the channel stays the same for each block but varies from one block to the next
Wireless/SDR

A Time-Varying Wireless Channel

Today we will discuss three strategies that are usually adopted for handling a wireless channel that is varying with time and hence acting differently on different data symbols. For a channel impulse response $c(t)$, number of multipath $N_{MP}$, channel gains $\gamma_i(t)$ and delays $\tau_i(t)$ for the $i$-th path, respectively, we can write \begin{equation*} c_B(t) = \sum _{i=0}^{N_{MP} -1} \gamma_i(t) \cdot \delta(t-\tau_i(t)) \end{equation*} i.e., channel gains $\gamma_i(t)$ and channel delays $\tau_i(t)$ are varying with time albeit at different rates. With the movement in the channel, the taps in a frequency selective channel are changing according to the rotation rates of path

Continue reading
DSP

Interpreting Time Domain Derivative in Frequency Domain

Although this article explains the concepts in terms of mathematical constants e and j as well as integration, my book on SDR steers clear of the complex notation and integrals to describe the underlying concepts from the ground up to an advanced level. One of the properties of Fourier Transform is that the derivative of a signal in time domain gets translated to multiplication of the signal spectrum by $j2\pi f$ in frequency domain. This property is usually derived as follows. For a signal $s(t)$ with Fourier Transform $S(f)$ \begin{equation*} s(t) = \frac{1}{2\pi}\int \limits _{-\infty}^{+\infty} S(f) e^{j2\pi ft}df, \end{equation*} we

Continue reading
Bandpass sampling
DSP

On Analog-to-Digital Converter (ADC), 6 dB SNR Gain per Bit, Oversampling and Undersampling

We have discussed before the sampling on time axis for analog to digital (A/D) conversion. An Analog to Digital Converter (ADC) produces the samples $x[n]$ of a continuous-time signal $x(t)$ at its input. Ideally, these samples are the exact values of the signal $x(t)$ at time instants $nT_s$ where $T_s=1/f_s$ is the sampling period. In practice, however, there are imperfections both on the y-axis and the x-axis. On y-axis, an ADC has a finite resolution depending on the number of bits used for quantization. On x-axis, there are issues of clock jitter that distort the samples produced. In this article,

Continue reading