Articles | Page 32 of 34

Block diagram of a pulse amplitude modulator and demodulator

July 24, 2016 Wireless/SDR

Pulse Amplitude Modulation (PAM)

In the article on modulation – from numbers to signals, we said that the Pulse Amplitude Modulation (PAM) is an amplitude scaling of the pulse $p(nT_S)$ according to the symbol value. What happens when this process of scaling the pulse amplitude by symbols is repeated for every symbol during each interval $T_M$? Clearly, a series of bits $b$ (1010 in our initial example) can be transmitted by choosing a rectangular pulse and scaling it with appropriate symbols. \begin{equation*} \begin{aligned} m = 0 \quad b = 1 \quad a[0] = +A \\ m = 1 \quad b = 0 \quad a[1]

July 29, 2016 DSP

Linear Systems

In wireless communications and other applications of digital signal processing, we often want to modify a generated or acquired signal. A device or algorithm that performs some prescribed operations on an input signal to generate an output signal is called a system. Amplifiers in communication receivers and filters in image processing applications are some systems that we interact with in daily lives. Our main focus in these articles will be on a particular class of systems which are linear and time-invariant. A linear system implies that if two inputs are scaled and summed together to form a new input, the

July 24, 2016 DSP

A Digital Signal

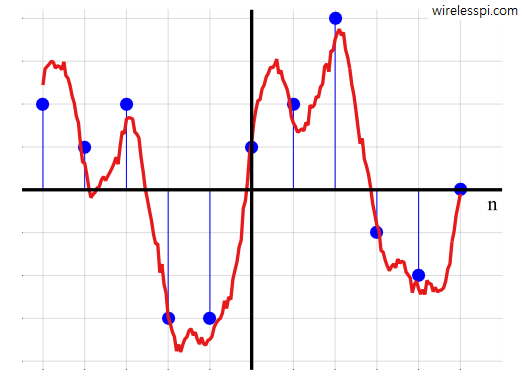
We have talked about obtaining a discrete-time signal through sampling the time-axis and obtaining a discrete frequency set through sampling the frequency axis. The same concept can be applied to the amplitude-axis, where the signal amplitude can be sampled to take only a finite set of discrete values. This discrete-time discrete-valued signal is called a digital signal, as opposed to an analog signal that is continuous in time and continuous in amplitude. The above figure shows how a digital signal having amplitudes over a fixed set of values can be obtained through slicing the underlying continuous amplitudes. For example, an

A BPSK constellation in a the presence of a carrier phase offset. A hypothetical QPSK constellation is also shown for comparison

July 23, 2016 Wireless/SDR

How to Detect a Carrier Lock in an SDR

We have discussed before the effect of a phase offset on the received signal. We have also seen a logical approach to solve this problem as well as one of the earliest algorithms for phase synchronization known as a Costas loop. Here, the purpose is to explain how a Rx detects whether the Phase Locked Loop (PLL) has acquired the lock. A receiver is simply a blind machine which can implement a PLL but can never get to know how it is actually doing. A lock detector is a logic signal used in the Rx to indicate successful synchronization after

July 21, 2016 DSP

Some DFT Properties

The purpose of this article is to summarize some useful DFT properties in a table. My favorite property is the beautiful symmetry depicted by continuous and discrete Fourier transforms. However, if you feel that this particular content is not as descriptive as the other posts on this website are, you are right. As opposed to the rest of the content on the website, we do not intend to derive all the properties here. Instead, based on what we have learned, some important properties of the DFT are summarized in the table below with an expectation that the reader can derive