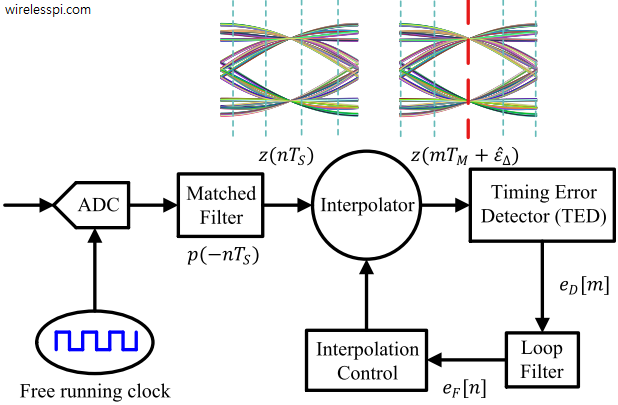
A Phase Locked Loop (PLL) for digital symbol timing recovery
Wireless/SDR

Phase Locked Loop (PLL) for Symbol Timing Recovery

A Phase Locked Loop (PLL) is a device used to synchronize a periodic waveform with a reference periodic waveform. It is an automatic control system in which the phase of the output signal is locked to the phase of the input reference signal. In the context of carrier phase synchronization, we talk about tracking the phase of an input reference sinusoid. For carrier frequency synchronization, a Frequency Locked Loop (FLL) is implemented. For the purpose of timing synchronization, the target is to adjust the timing phase of a receiver clock to that of the transmitter clock such that one sample/symbol

Continue reading
A signal broken down into scaled and shifted impulses
DSP

Convolution

Understanding convolution is the biggest test DSP learners face. After knowing about what a system is, its types and its impulse response, one wonders if there is any method through which an output signal of a system can be determined for a given input signal. Convolution is the answer to that question, provided that the system is linear and time-invariant (LTI). We start with real signals and LTI systems with real impulse responses. The case of complex signals and systems will be discussed later. Convolution of Real Signals Assume that we have an arbitrary signal $s[n]$. Then, $s[n]$ can be

Continue reading
A channel with 8 taps demonstrating the main cursor, precursor ISI and postcursor ISI
Wireless/SDR

How Decision Feedback Equalizers (DFE) Work

We started the classification of equalization algorithms by introducing the need for equalization in wireless communication systems. We said that the wireless channel is a source of severe distortion in the received (Rx) signal and our main task is to remove the resulting Inter-Symbol Interference (ISI) from the Rx samples. Equalization refers to any signal processing technique in general and filtering in particular that is designed to eliminate or reduce this ISI before symbol detection. In essence, the output of an equalizer should be a Nyquist pulse for a single symbol case. A conceptual block diagram of the equalization process

Continue reading
A prism decomposes the white light into 7 colors
DSP

The Discrete Fourier Transform (DFT)

Learned in some other articles on this website, the following three important concepts take us to the core of the Discrete Fourier Transform (DFT) idea. Regardless of the signal shape, most signals of practical interest can be considered as a sum of complex sinusoids oscillating at different frequencies. A set of $N$ orthogonal complex sinusoids can be constructed within a span of $N$ time domain samples. Each `tick’ or bin on the discrete frequency axis denotes the discrete frequency $k/N$ of such a complex sinusoid. To understand how a set of sinusoids with $N$ discrete frequencies can sum up to

Continue reading
Block diagram of a 4 symbol communication system
Wireless/SDR

Packing More Bits in One Symbol

Note that digital electronics are constrained to work on only two levels by electronic switches which in the simplest case are either on or off. For many reasons, practical digital communication systems require quite complicated signal processing workload both at the Tx and Rx ends that can be performed only by a device more intelligent than an electronic switch, such as an Application Specific Integrated Circuit (ASIC), Field Programmable Gate Array (FPGA), Digital Signal Processor (DSP) or a General Purpose Processor (GPP). If this intelligent device can differentiate between two signal levels like a switch, it can certainly differentiate between

Continue reading