Articles | Page 29 of 35

Setup for Differential Phase Difference of Arrival (DPDoA)

June 27, 2022 Localization

Location Estimation through Differential Phase Difference of Arrival

In an article on carrier phase based ranging, we saw how phase observations were employed to find the range between two wireless devices. Today we explore how phase can also be used for the purpose of location estimation. Background To determine the position of a wireless device, its range needs to be computed from a set of anchor nodes. When these anchors and the device itself are synchronized with each other, the signal propagation time of an electromagnetic wave arriving at these anchors after its emission from a Tx can be employed to calculate the corresponding distances. This is the

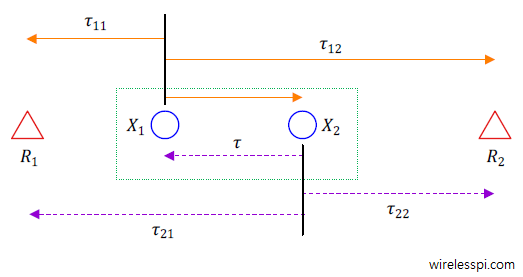
Magnitude of frequency response |H[k]| in response to complex sinusoids at all N frequencies

August 12, 2016 DSP

System Characterization

In wireless communications and other applications of digital signal processing, we often want to modify a generated or acquired signal. A device or algorithm that performs some prescribed operations on an input signal to generate an output signal is called a system. In another article about transforming a signal, we saw how a signal can be scaled and time shifted, or added and multiplied with another signal. These are all examples of a system. Amplifiers in communication receivers and filters in image processing applications are some systems that we interact with in daily lives. A communication channel is also a

Computing noise power within a specified bandwidth

August 15, 2016 Wireless/SDR

Additive White Gaussian Noise (AWGN)

The performance of a digital communication system is quantified by the probability of bit detection errors in the presence of thermal noise. In the context of wireless communications, the main source of thermal noise is addition of random signals arising from the vibration of atoms in the receiver electronics. You can also watch the video below. The term additive white Gaussian noise (AWGN) originates due to the following reasons: [Additive] The noise is additive, i.e., the received signal is equal to the transmitted signal plus noise. This gives the most widely used equality in communication systems. \begin{equation}\label{eqIntroductionAWGNadditive} r(t) = s(t)

Coverage and throughput in different bands

December 20, 2021 Wireless/SDR

Channel Propagation Effects in mmWave Systems

In a previous article, we have discussed in detail the free space propagation in mmWave systems. We saw that the received power at any distance is independent of the carrier frequency as long as the effective antenna aperture is taken into account. Today, we describe the role of atmospheric effects such as water vapors, oxygen, rain and penetration loss in materials that impact the signal propagation at higher carrier frequencies. Important parameters of small-scale fading in a wireless channel such as delay spread and Doppler spread are also explained in the context of mmWave systems. Atmospheric Effects In realistic channels,

August 14, 2016 Wireless/SDR

Modulation – From Numbers to Signals

The purpose of digital communications is to send digital data across a channel which can be wireless telephone lines coaxial cable optical fiber Ethernet USB chips on a printed circuit board Considering the examples shown in Figure above, clearly neither a bit sequence nor a symbol sequence can be transmitted on their own through these channels — as they are nothing more than a set of numbers. Therefore, a signal waveform is an appropriate tool that can travel down the channel and carry the required information — just like a train running on its track and carrying the load. For