Modulation – From Numbers to Signals

The purpose of digital communications is to send digital data across a channel which can be

• wireless
• telephone lines
• coaxial cable
• optical fiber
• Ethernet
• USB
• chips on a printed circuit board

Considering the examples shown in Figure above, clearly neither a bit sequence nor a symbol sequence can be transmitted on their own through these channels — as they are nothing more than a set of numbers. Therefore, a signal waveform is an appropriate tool that can travel down the channel and carry the required information — just like a train running on its track and carrying the load.

For this purpose, the symbol sequence needs to be converted into an analog waveform that suits the characteristics of that particular channel. Let us start with a simple example.

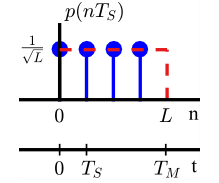
Assume a rectangular pulse shape $p(nT_S)$ (technically, it is called Non Return to Zero (NRZ) pulse shape but we will continue using the term rectangular for ease of visualization) shown in Figure above whose length is equal to one symbol interval in continuous-time, $T_M$ = $LT_S$. However, observe that an interval of length $LT_S$ seconds is not the same as the interval covered by $L$ samples with a separation of $T_S$ seconds between them. In discrete-time, the pulse length contains $L$ samples with a total length of $(L-1)T_S$ seconds but the missing sample in the end is the same as the first sample of the next pulse if they were transmitted in a continuous stream.

During each symbol interval $T_M$, some characteristic of $p(nT_S)$ can be altered to make it a function of the symbol sequence $a[m]$. This process is called modulation. The amplitude of the pulse is one such candidate that can be varied according to the symbol values.

Note that the pulse energy without any normalization constant is given by $\sum _{n=0}^{L-1}$ $1^2$ $= L$. To make the system independent of the pulse amplitude itself, it can be normalized with $1/\sqrt{L}$ as shown in Figure above, thus turning it into a unit energy pulse.
\begin{align*}
E_p &= \sum \limits _{n=0}^{L-1} \left(\frac{1}{\sqrt{L}}\right)^2 = 1
\end{align*}

Let us now relate the bit rate $R_b$ with the symbol rate $R_M$ and sample rate $R_S$. Typically, data bits 0 and 1 are generated with equal probability at a rate of $R_b = 1/T_b$ b/s. In our simple scenario, a 0 is represented by symbol $-A$ and a 1 by symbol $+A$ and the symbol rate is denoted as $R_M = 1/T_M$. Here, $T_b$ and $T_M$ are equal due to a single bit for every symbol duration. Subsequently, a pulse shape at a sample rate of $F_S = 1/T_S$ is generated with number of samples
\begin{equation}\label{eqCommSystemSamplesSymbol}
L = \frac{T_M}{T_S} = \frac{F_S}{R_M}
\end{equation}
This parameter $L$ is known as samples/symbol, or sample rate normalized to symbol rate, or oversampling factor. It is standard practice to select an integer $L$ so that the sample rate is an integer multiple of the symbol rate.

The amplitude of the pulse $p(nT_S)$ can be multiplied with $-A$ for transmitting a 0 and with $+A$ for transmitting a 1. As a consequence, two scaled versions of that pulse shape $s_0(nT_S)$ and $s_1(nT_S)$ are created whose amplitudes bear the symbol levels $-A$ and $+A$ representing 0 and 1, respectively. This amplitude scaling of the pulse $p(nT_S)$ according to the symbol value is called Pulse Amplitude Modulation (PAM) and is illustrated in Figure below.

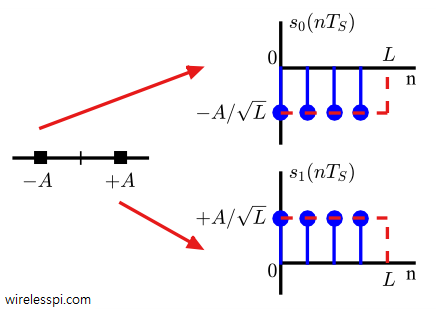
This can be seen as a natural result of holding the amplitude constant at a symbol level for the duration of a symbol $T_M$. Mathematically,

\begin{align}\label{eqCommSystemPAM}
s_0(nT_S) &= -A \cdot p(nT_S) \\
s_1(nT_S) &= +A \cdot p(nT_S)
\end{align}

During the transmission, the signal is corrupted by Additive White Gaussian Noise (AWGN) with power spectral density $N_0/2$ Watt/Hz. The received signal can be expressed as
\begin{equation*}
r(nT_S) = \left\{ \begin{array}{l}
s_0(nT_S) + w(nT_S), \quad b = 0, \\
s_1(nT_S) + w(nT_S), \quad b = 1, \\
\end{array} ~~ \quad 0 \le n \le L-1 \right.
\end{equation*}

The task of the receiver is to find the most probable symbol in the interval $0 \le n \le L-1$ and hence determine whether a 0 or a 1 was transmitted.