Articles | Page 28 of 35

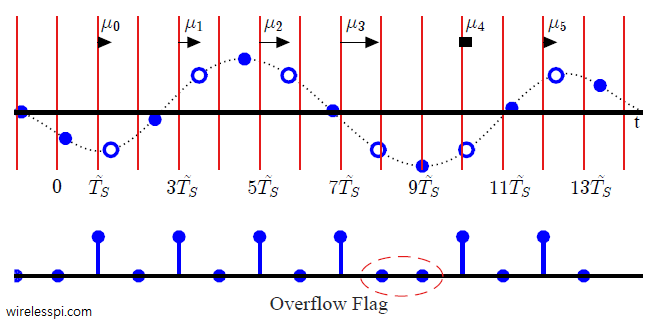
Due to a Sampling Clock Offset (SCO), a fast Rx clock collects extra samples

January 10, 2022 Wireless/SDR

Effect of Sampling Clock Offset on a Single-Carrier Waveform

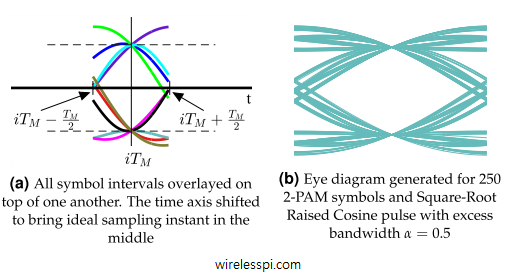
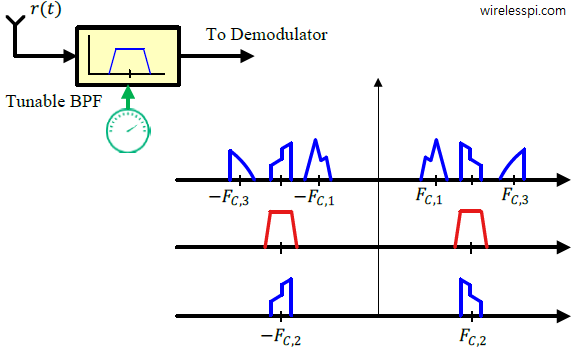
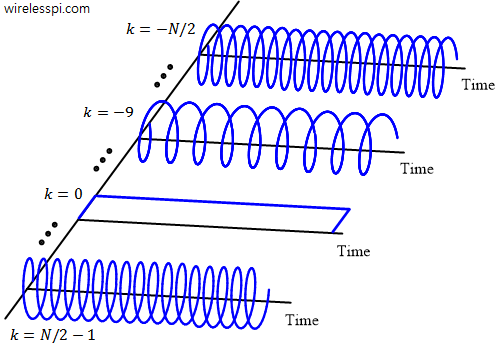
We have discussed before the distortion caused by a symbol timing offset on the communication waveform. We have also derived a maximum likelihood estimate of the clock phase offset. In this article, we describe the impact of a sampling clock offset in a single-carrier waveform, also commonly known as a clock frequency offset or timing drift. A clock frequency offset is defined as the rate mismatch between the Tx and Rx clocks. Just like a carrier phase and frequency offset, the clock used to sample the incoming continuous-time signal at a rate $T_S=1/F_S$ contains a phase and frequency offset as

All symbol intervals are overlayed on top of one another and the time axis is shifted to bring ideal sampling instant in the middle. Eye diagram generated for 250 2-PAM symbols and Square-Root Raised Cosine pulse with excess bandwidth 0.5

August 21, 2016 DSP

Tools for Signal Diagnosis

In this article, we will devise some tools that help us diagnose problems with the communication system under study. I like to call them the stethoscopes for a communication system due to the crucial functionality they provide regarding the health of the communication system being analyzed. We discuss three such tools, namely an eye diagram, a transition diagram and a scatter plot below. Eye Diagram An eye diagram is an excellent summary of the signal behaviour in time domain, something analogous to a spectrum in frequency domain. Imagine the samples of the matched filter output taken at a much higher

A Tuned radio Frequency Receiver (TRF) selects the desired channel through a bandpass filter

February 21, 2022 Wireless/SDR

Tuned Radio Frequency (TRF) Receiver

The tasks of a communications receiver to demodulate the transmitted signal begin with selecting the signal within a specific bandwidth at a desired frequency, commonly known as a particular channel. In another article, we discuss specifications for a radio receiver such as dynamic range, noise floor and sensitivity. Today we discuss an architecture used in earlier generations of radios. To avoid interference from the neighboring channels, the most straightforward approach is to filter out the spectral contents outside this channel and amplify the desired signal in one or more RF amplification stages. This was one of the earliest techniques employed

July 3, 2018 Wireless/SDR

The Arrival of 6G

Recently, IEEE Communications Society published an article “What will 6G be?” Some of the important points it highlighted are the following. More spectrum is needed for more bits: As with all new Gs, more spectrum is needed to entertain more bits 🙂 Sometimes I wonder where exactly we have made a phenomenal progress in delivering orders of magnitude higher data rates. According to Gerhard Fettweis, several bands between 100 and 300 GHz show some promise. Bits/s/$m^3$: Since the success of a company is measured in the revenue generated, and not exactly the bits delivered per second, the real focus is

August 18, 2016 DSP

Discrete Frequency

An Analog to Digital Converter (ADC) samples a continuous-time signal to produce discrete-time samples. For a digital signal processor, this signal just resides in memory as a sequence of numbers. Consequently, the knowledge of the sample rate $F_S$ is the key to signal manipulation in digital domain. As far as time is concerned, one can easily determine the period or frequency of such a signal stored in the memory. For example, the period $T$ in the sinusoid of Figure below is clearly $10$ samples and sample time $T_S=1/F_S$ can be employed to find its period in seconds. For a sample