Basics Archives | Page 3 of 3

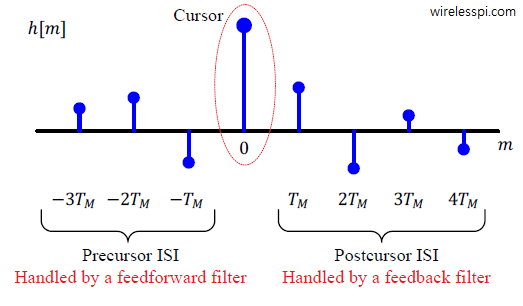
A channel with 8 taps demonstrating the main cursor, precursor ISI and postcursor ISI

January 31, 2022 Wireless/SDR

How Decision Feedback Equalizers (DFE) Work

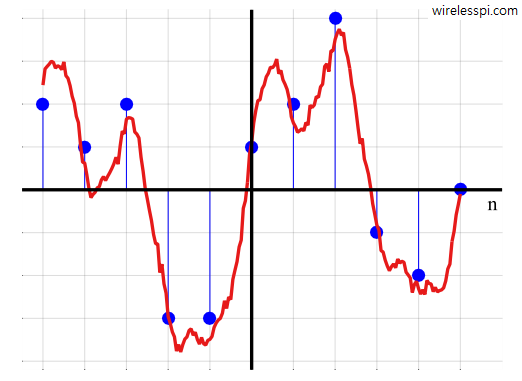
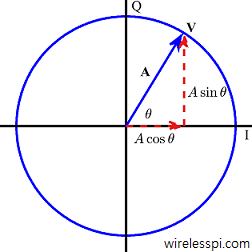
We started the classification of equalization algorithms by introducing the need for equalization in wireless communication systems. We said that the wireless channel is a source of severe distortion in the received (Rx) signal and our main task is to remove the resulting Inter-Symbol Interference (ISI) from the Rx samples. Equalization refers to any signal processing technique in general and filtering in particular that is designed to eliminate or reduce this ISI before symbol detection. In essence, the output of an equalizer should be a Nyquist pulse for a single symbol case. A conceptual block diagram of the equalization process

July 24, 2016 DSP

A Digital Signal

We have talked about obtaining a discrete-time signal through sampling the time-axis and obtaining a discrete frequency set through sampling the frequency axis. The same concept can be applied to the amplitude-axis, where the signal amplitude can be sampled to take only a finite set of discrete values. This discrete-time discrete-valued signal is called a digital signal, as opposed to an analog signal that is continuous in time and continuous in amplitude. The above figure shows how a digital signal having amplitudes over a fixed set of values can be obtained through slicing the underlying continuous amplitudes. For example, an

July 1, 2016 DSP

What is a Signal?

In traditional Digital Signal Processing (DSP) courses, we usually learn about signals in a narrow context. While this is probably the correct approach for an introduction to this field, there is a broader theme to the concept of signals. Let us focus on the purely technical part first. A signal is any measurable quantity that varies with time (or some other independent variable). If you record the words you speak in a computer memory and plot against time, you get a speech signal. As an example, the figure below shows a signal for the words "Hello Wireless" recorded in a

A complex number with its I and Q components

July 4, 2016 DSP

Dealing with Complex Numbers

Although complex notation is not complex to understand, I attempt to avoid complex notation altogether while writing DSP articles. If you are interested in where these complex numbers come from, you can read my real-imaginative guide to complex numbers. A complex number is defined as an ordered pair of real numbers in $(x,y)$-plane. In that respect, complex numbers can be considered as vectors with initial point on the origin $(0,0)$. Addition of complex numbers is then similar to the addition of vectors in $(x,y)$-plane from this perspective. However, multiplication is well defined for complex numbers while it is not defined