In traditional Digital Signal Processing (DSP) courses, we usually learn about signals in a narrow context. While this is probably the correct approach for an introduction to this field, there is a broader theme to the concept of signals. Let us focus on the purely technical part first.
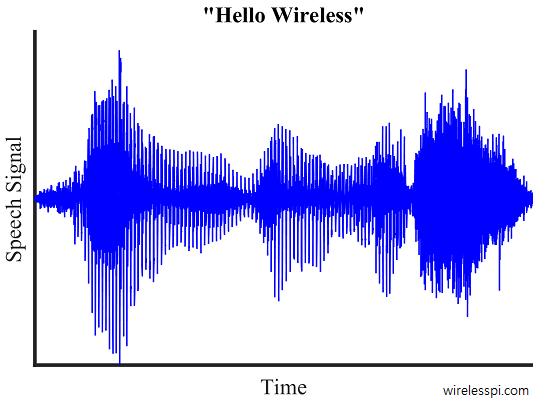
A signal is any measurable quantity that varies with time (or some other independent variable). If you record the words you speak in a computer memory and plot against time, you get a speech signal. As an example, the figure below shows a signal for the words "Hello Wireless" recorded in a computer.
Some familiar signals from everyday life are
- temperature or pressure readings,
- GPS signals that determine your vehicle’s position,
- biological signals like EEG and ECG that are electrical activity recordings of the brain and heart, respectively, and
- stock prices that reflect the expectations of corporate earnings.
Mathematically speaking, a signal is a function of an independent variable. For example, a function $s(t) = 3t^2$ can be considered as a signal varying quadratically with time.
In these articles, we will focus on signals comprising of one independent variable and one dependent variable. The independent variable on x-axis is usually labeled as time, while the value of the signal at each time instant is called amplitude.
With these technical definitions in place, we can expand our view of signals that encompasses almost everything in our universe. The universe started from a singularity with all the matter and energy we see around us compressed into a tiny dot smaller than an atom. Since then, everything that moves or jiggles is generating signals all the time. Some examples are the spinning of galaxies, stars and planets, their internal chemical activity, heat and storm patterns, light and electromagnetic waves, temperature variations and ocean currents. Even all living organisms are signal processing machines in the sense that they rely on signals to interpret their environment and adjust their behaviour. We like to think of signals only as an electrical activity because the desired processing is done in electronic computers and transducers are used to convert real world phenomenon in the form of electrical signals. If we could invent magnetic computers, then we would mostly be interpreting signals around us as magnetic patterns.
Human activity also produces signals in a continuous manner such as our breathing patterns, optical signals entering our brains through our eyes and even our driving patterns in rush hour. Even simple actions like thinking a thought gives rise to new signals. Some other signals arising form societal interactions are also of interest to us such as a player’s performance (in numbers) in a sport, bank statements and financial data. I think that future scientists will be able to map love to some sort of signal as well. This is because mathematics is the language of the universe and most phenomena starting from the violent storms in a star to the rise and fall of our emotions due to hormonal variations can be mapped to numbers.
With these numbers in hand, Digital Signal Processing (DSP) is simply a skill or a toolkit to deal with these number sequences. It comprises of various tools and techniques that enable us to view the same number patterns through different lenses and operate on them by using efficient algorithms. Even machine learning is a kind of DSP that utilizes advanced mathematical techniques to manipulate and utilize data sets.
In summary, everything that moves or jiggles generates signals; and every signal can be represented by numbers; and all number sequences can be manipulated by algorithms. If mathematics is the language of the universe, then algorithms are the songs in that language. You can read more about some basic signals here.