OFDM Archives | Page 2 of 3

February 14, 2022 Wireless/SDR

Advantages and Disadvantages of OFDM – A Summary

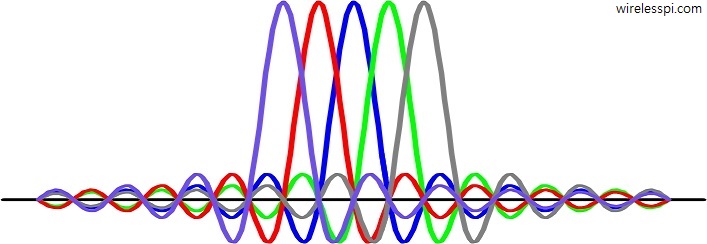
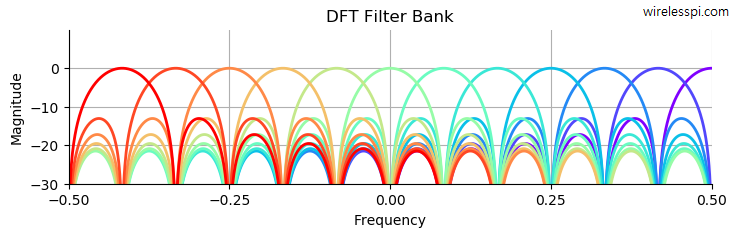
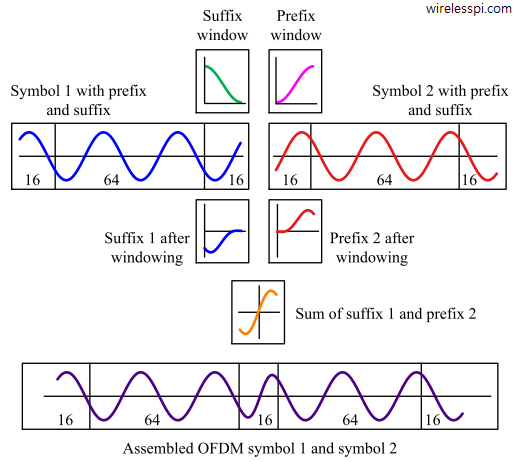
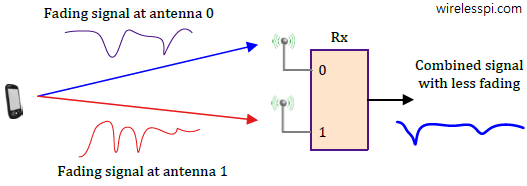
Orthogonal Frequency Division Multiplexing (OFDM) is a technique of choice for many high rate wireless communication systems. An overview of OFDM for a DSP/wireless beginner was given in this article where visualizations of how OFDM slices the spectrum into multiple subcarriers for one user was provided in detail. Orthogonal Frequency Division Multiple Access (OFDMA) is an extension of OFDM for multiple users, i.e., it is a multiple access technology (like TDMA and CDMA from 2G and 3G cellular systems, respectively) in which the available spectrum is divided into multiple subcarriers that are shared among multiple users. This was the choice

A bank of N filters each centered at discrete frequency k/N

March 19, 2020 DSP

Discrete Fourier Transform (DFT) as a Filter Bank

We have discussed before what a Discrete Fourier Transform (DFT) is and how to find the DFT of some commonly used signals. Here, we will see how a DFT acts as a (crude) bank of filters that can pass the signal contents around a desired frequency while blocking the rest. Let us start with the definition of the DFT. \begin{equation*} \begin{aligned} S_I[k]\: &= \sum \limits _{n=0} ^{N-1}\left[ s_I[n] \cos 2\pi\frac{k}{N}n + s_Q[n] \sin 2\pi\frac{k}{N}n\right] \\ S_Q[k] &= \sum \limits _{n=0} ^{N-1}\left[ s_Q[n] \cos 2\pi\frac{ k}{N}n – s_I[n] \sin 2\pi\frac{k}{N}n\right] \end{aligned} \end{equation*} for each $k$. In complex notation, this DFT is

At the boundary of two OFDM symbols, pulse shaping smoothes the edges, resulting in the avoidance of spectral regrowth

February 26, 2020 Wireless/SDR

Windowing an OFDM Signal in Time Domain

Orthogonal Frequency Division Multiplexing (OFDM) has been introduced in a previous article as a technique suitable for high data-rate transmissions over a wireless channel. The two main advantages I mentioned were as follows: Simple one-tap equalization, and Ability to slice the spectrum and utilize each slice in an independent manner. Due to these advantages, it was adopted as the preferred modulation in WiFi and 4G-LTE systems. The interesting part is that while many new waveforms were proposed to replace it in 5G NR, OFDM was still the modulation of choice for both downlink and uplink directions with some minor changes.

Diversity implies two or more independent replicas of the same information

November 2, 2021 Wireless/SDR

Multiple Antenna Techniques

When computing approaches the physical limits of clocking speeds, we turn towards multi-core architectures. When communication approaches the physical limits of transmission speeds, we turn towards multi-antenna systems. What exactly are the benefits that led to scientists and engineers choosing multiple antennas as the foundation of 4G and 5G PHY layers? While having spatial diversity was the original incentive for adding antennas at the base stations, it was discovered in mid 1990s that multiple antennas at Tx and/or Rx sides open up other possibilities not foreseen in single antenna systems. Let us now describe three main techniques in this context.

OFDM slices the spectrum just like a bread

May 1, 2017 Wireless/SDR

A Beginner’s Guide to OFDM

In the recent past, high data rate wireless communications is often considered synonymous to an Orthogonal Frequency Division Multiplexing (OFDM) system. OFDM is a special case of multi-carrier communication as opposed to a conventional single-carrier system. The concepts on which OFDM is based are so simple that almost everyone in the wireless community is a technical expert in this subject. However, I have always felt an absence of a really simple guide on how OFDM works which can prove useful for technical persons not wanting to deal with too much technicalities, such as DSP experts outside communications, computer programmers, ham