Tag: Software Defined Radio (SDR)

Wired and wireless channels
Wireless/SDR

Modulation – From Numbers to Signals

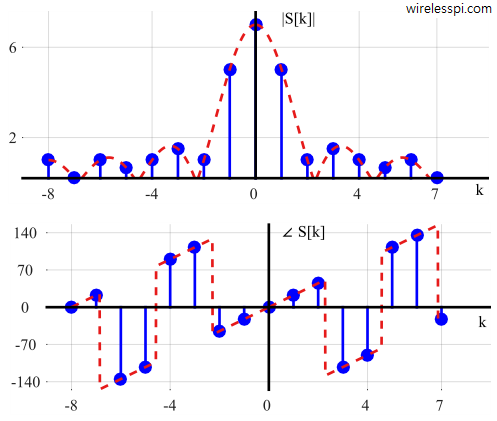
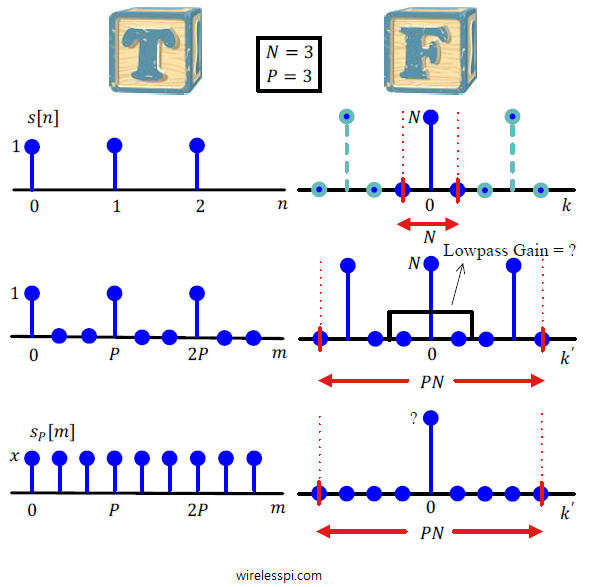
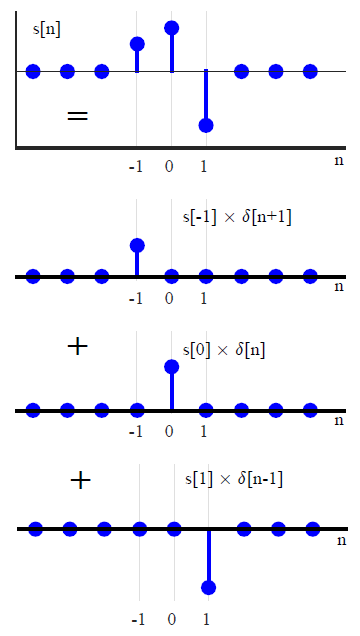
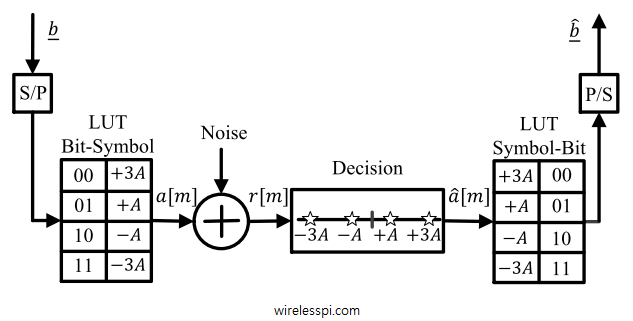
The purpose of digital communications is to send digital data across a channel which can be wireless telephone lines coaxial cable optical fiber Ethernet USB chips on a printed circuit board Considering the examples shown in Figure above, clearly neither a bit sequence nor a symbol sequence can be transmitted on their own through these channels — as they are nothing more than a set of numbers. Therefore, a signal waveform is an appropriate tool that can travel down the channel and carry the required information — just like a train running on its track and carrying the load. For

Continue reading
Magnitude and phase of the DFT of a rectangular signal for L = 7, N= 16 and starting sample shifted by one
DSP

DFT Examples

For understanding what follows, we need to refer to the Discrete Fourier Transform (DFT) and the effect of time shift in frequency domain first. Here, we discuss a few examples of DFTs of some basic signals that will help not only understand the Fourier transform but will also be useful in comprehending concepts discussed further. A Rectangular Signal A rectangular sequence, both in time and frequency domains, is by far the most important signal encountered in digital signal processing. One of the reasons is that any signal with a finite duration, say $T$ seconds, in time domain (that all practical

Continue reading
A rectangular signal and its upsampled version in time and frequency domains
DSP

Sample Rate Conversion

In the discussion on sampling, the process of sampling a continuous-time signal was discussed in detail and subsequently sampling theorem was derived. In many applications, resampling an already digitized signal is mandatory for an efficient system design. In wireless communications, sample rate conversion is utilized for upconversion and downconversion to a desired frequency, filtering stages in the digital frontend and sometimes for carrier and timing synchronization during signal acquisition. See the Cascade Integrator Comb (CIC) filters for how to accomplish this task with minimal resources. In discrete domain, sample rate can be reduced by discarding intermediate samples periodically called downsampling

Continue reading
A signal broken down into scaled and shifted impulses
DSP

Convolution

Understanding convolution is the biggest test DSP learners face. After knowing about what a system is, its types and its impulse response, one wonders if there is any method through which an output signal of a system can be determined for a given input signal. Convolution is the answer to that question, provided that the system is linear and time-invariant (LTI). We start with real signals and LTI systems with real impulse responses. The case of complex signals and systems will be discussed later. Convolution of Real Signals Assume that we have an arbitrary signal $s[n]$. Then, $s[n]$ can be

Continue reading
Block diagram of a 4 symbol communication system
Wireless/SDR

Packing More Bits in One Symbol

Note that digital electronics are constrained to work on only two levels by electronic switches which in the simplest case are either on or off. For many reasons, practical digital communication systems require quite complicated signal processing workload both at the Tx and Rx ends that can be performed only by a device more intelligent than an electronic switch, such as an Application Specific Integrated Circuit (ASIC), Field Programmable Gate Array (FPGA), Digital Signal Processor (DSP) or a General Purpose Processor (GPP). If this intelligent device can differentiate between two signal levels like a switch, it can certainly differentiate between

Continue reading