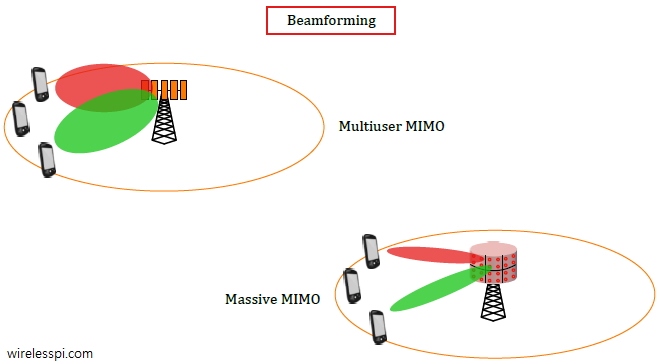
Massive MIMO is one of the defining technologies in 5G cellular systems. In a previous article, we have described spatial matched filtering (or maximum ratio) as the simplest algorithm for signal detection. Here, we explain another linear technique, known as Zero-Forcing (ZF), for this purpose. It was described before in the context of simple MIMO systems here. Background Consider the block diagram for uplink of a massive MIMO system as drawn below with $N_B$ base station antennas and $K$ mobiler terminals. It is evident that the cumulative signal at each base station antenna $j$ is a summation of signals arriving
Continue reading