Software Defined Radio (SDR) Archives | Page 4 of 5

July 30, 2016 DSP

Correlation

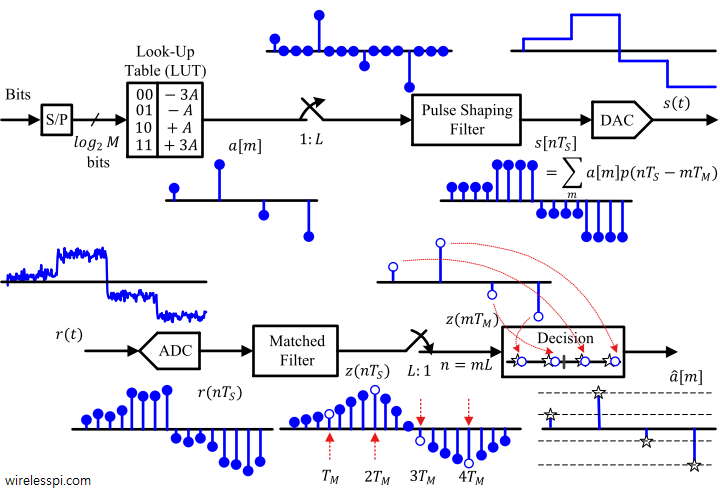
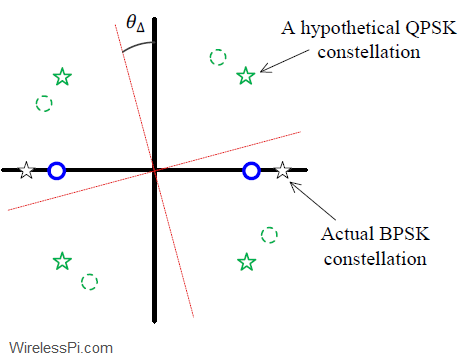
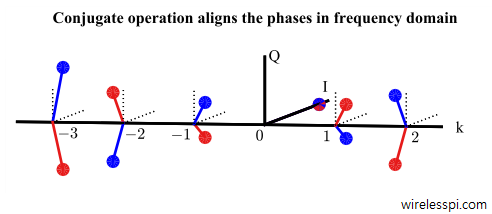
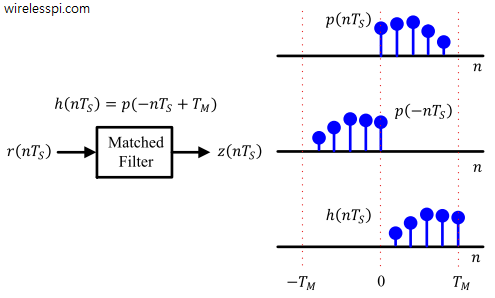
Correlation is a foundation over which the whole structure of digital communications is built. In fact, correlation is the heart of a digital communication system, not only for data detection but for parameter estimation of various kinds as well. Throughout, we will find recurring reminders of this fact. As a start, consider from the article on Discrete Fourier Transform that each DFT output $S[k]$ is just a sum of term-by-term products between an input signal and a cosine/sine wave, which is actually a computation of correlation. Later, we will learn that to detect the transmitted bits at the receiver, correlation

Block diagram of a pulse amplitude modulator and demodulator

July 24, 2016 Wireless/SDR

Pulse Amplitude Modulation (PAM)

In the article on modulation – from numbers to signals, we said that the Pulse Amplitude Modulation (PAM) is an amplitude scaling of the pulse $p(nT_S)$ according to the symbol value. What happens when this process of scaling the pulse amplitude by symbols is repeated for every symbol during each interval $T_M$? Clearly, a series of bits $b$ (1010 in our initial example) can be transmitted by choosing a rectangular pulse and scaling it with appropriate symbols. \begin{equation*} \begin{aligned} m = 0 \quad b = 1 \quad a[0] = +A \\ m = 1 \quad b = 0 \quad a[1]

A BPSK constellation in a the presence of a carrier phase offset. A hypothetical QPSK constellation is also shown for comparison

July 23, 2016 Wireless/SDR

How to Detect a Carrier Lock in an SDR

We have discussed before the effect of a phase offset on the received signal. We have also seen a logical approach to solve this problem as well as one of the earliest algorithms for phase synchronization known as a Costas loop. Here, the purpose is to explain how a Rx detects whether the Phase Locked Loop (PLL) has acquired the lock. A receiver is simply a blind machine which can implement a PLL but can never get to know how it is actually doing. A lock detector is a logic signal used in the Rx to indicate successful synchronization after

The blue line is the signal template and while red is the matched filter. Notice the same magnitude on each spectral line but exactly opposite phase

July 18, 2016 DSP / Wireless/SDR

Demodulation – From Signals Back to Numbers

Remember that in the article on correlation, we discussed that correlation of a signal with proper normalization is maximum with itself and lesser for all other signals. Since the number of possible signals is limited in a digital communication system, we can use the correlation between incoming signal $r(nT_S)$ and possible choices $s_0(nT_S)$ and $s_1(nT_S)$ in a digital receiver. Consequently, a decision can be made in favor of the one with higher correlation. It turns out that the theory of maximum likelihood detection formalizes this conclusion that it is the optimum receiver in terms of minimizing the probability of error.

July 8, 2016 DSP / Wireless/SDR

Convoluted Correlation between Matched Filter and Correlator

Now we turn out attention towards a topic that causes a lot of confusion for communications and DSP learners: what is the difference between a matched filter and a correlator in a communications receiver? Let us start with the definition of a correlator: A correlator is a device that performs correlation of a received signal with its template within a given window of time. In our context, that window of time is the symbol duration, $T_M$. So a correlator performs the following operations. It takes this sample-by-sample product and sums them together. Next, it samples the output of this accumulation