Timing Recovery Archives | Page 3 of 4

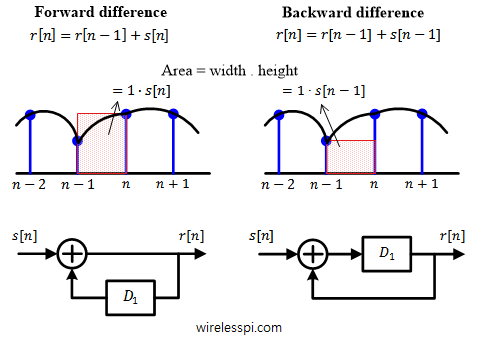
A discrete-time integrator implemented through a forward difference and a backward difference technique

September 15, 2017 DSP

Discrete-Time Integrators

An integrator is a very important filter that proves useful in implementation of many blocks of a communication receiver such as symbol timing synchronization and Phase-Locked Loop (PLL). It is an inverse operation to a differentiator that is also used in many signal processing applications such as FM demodulation and image processing. In continuous-time case, an integrator finds the area under the curve of a signal amplitude. A discrete-time system deals with just the signal samples and hence a discrete-time integrator serves the purpose of collecting a running sum of past samples for an input signal. Looking at an infinitesimally

Known training sequence (a preamble) is prepended, or training can also be inserted periodically within the message

January 13, 2017 Wireless/SDR

Basics of Synchronization

In every digital communication system, the Tx has the easier role of signal generation while the Rx has the tougher job of figuring out the intended message. Just like solving a puzzle told by someone. Estimating and compensating for the frequency, phase and timing offsets between Tx and Rx oscillators is one such challenge. The solution can be designed depending on many factors such as some part of data is known (called a ‘training sequence’) or not, the synchronizer needs to be one-shot or continuously updating, and so on. Known Data Availability Depending on the availability of known data, synchronization

December 2, 2016 DSP / Machine Learning

The Master Algorithm

Recently, I was reading the book The Master Algorithm by Pedro Domingos — a Professor at the University of Washington in machine learning. According to the description of his book, The Master Algorithm in Machine Learning A spell-binding quest for the one algorithm capable of deriving all knowledge from data, including a cure for cancer. Society is changing, one learning algorithm at a time, from search engines to online dating, personalized medicine to predicting the stock market. But learning algorithms are not just about Big Data – these algorithms take raw data and make it useful by creating more algorithms.

Phase jumps at every zero crossing from modulating data onto the carrier phase for a QPSK waveform

October 7, 2016 Wireless/SDR

The Fundamental Problem of Synchronization

We have seen in the effect of phase rotation that the matched filter outputs do not map back perfectly onto the expected constellation, even in the absence of noise and no other distortion. Unless this rotation is small enough, it causes the symbol-spaced optimal samples to cross the decision boundary and fall in the wrong decision zone. And even for small rotations, relatively less amount of noise can cause decision errors in this case, i.e., noise margin is reduced. In fact, for higher-order modulation, the rotation becomes even worse because the signals are closely spaced with each other for the

A general QAM detector with respective waveforms at each block

October 7, 2016 Wireless/SDR

Quadrature Amplitude Modulation (QAM)

Quadrature Amplitude Modulation (QAM) is a spectrally efficient modulation scheme used in most of the high-speed wireless networks today. We discussed earlier that Pulse Amplitude Modulation (PAM) transmits information through amplitude scaling of the pulse $p(nT_S)$ according to the symbol value. To understand QAM, two routes need to be traversed. Route 1 We start the first route with differentiating between baseband and passband signals. A baseband signal has a spectral magnitude that is nonzero only for frequencies around origin ($F=0$) and negligible elsewhere. An example spectral plot for a PAM waveform is shown below for 500 2-PAM symbols shaped by