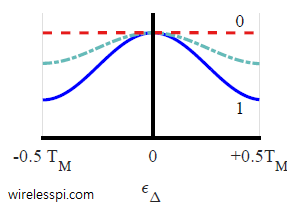
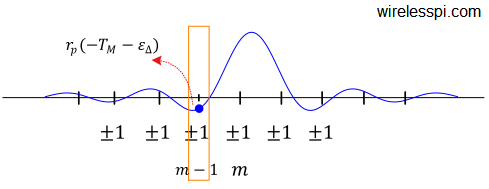
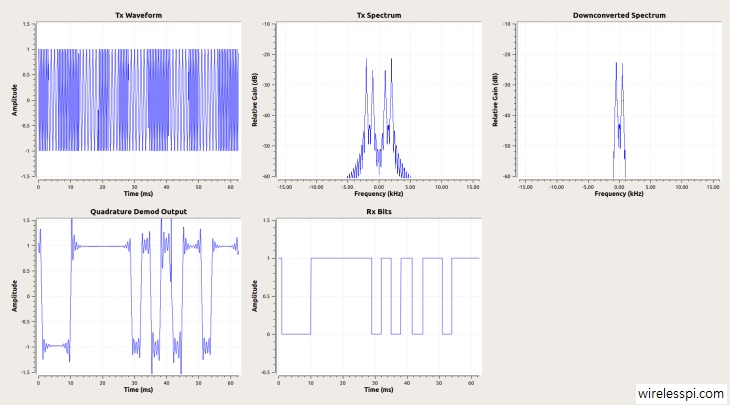
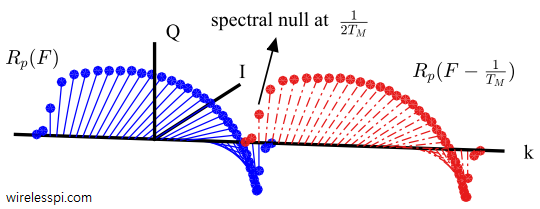
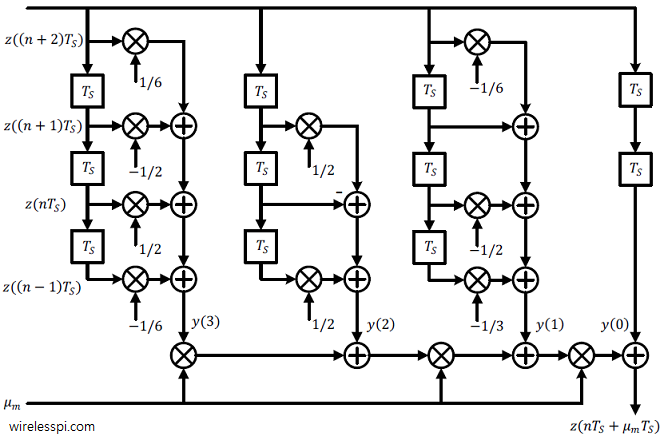
In an article on Phase Locked Loop (PLL) for symbol timing recovery, we described an intuitive view of a maximum likelihood Timing Error Detector (TED). We saw that the timing matched filter is constructed by computing the derivative of the matched filter and consequently its output is the derivative of the input signal. Naturally, this output is more fine-grained and hence accurate when the number of samples/symbol $L$ is large. Here, $L$ must be several times larger than the minimum limit set by the Nyquist theorem. However, in most applications, reducing the complexity of the timing locked loop is far
Continue readingTag: Timing Recovery
Mueller and Muller Timing Synchronization Algorithm
Proposed in 1976, Mueller and Muller algorithm is a timing synchronization technique that operates at symbol rate, as opposed to most other synchronization algorithms that require at least 2 samples/symbol such as early-late and Gardner timing error detectors. All of these are feedback techniques that operate within a PLL. Feedforward methods such as digital filter and square timing synchronization are also feasible due to powerful digital signal processing that avoids feedback problems such as hangups. The most confusing thing communication engineers and radio hobbyists find about Mueller and Muller algorithm algorithm is the cross product in its expression: matched filter
Continue reading
FSK Demodulation in GNU Radio
Frequency Modulation (FM) is one of the oldest communication techniques for high fidelity transmission. Its digital counterpart, Frequency Shift Keying (FSK), also plays a crucial role in applications requiring low receiver complexity. In an FSK scheme, digital information is transmitted by changing the frequency of a carrier signal. It can also be mixed with Chirp Spread Spectrum (CSS) for low-power long-range communication as used in LoRa PHY. Binary FSK Binary FSK (BFSK) is the simplest form of FSK where the two bits 0 and 1 correspond to two distinct carrier frequencies $F_0$ and $F_1$ to be sent over the air.
Continue reading
What is a Symbol Timing Offset and How It Distorts the Rx Signal
Timing synchronization is one of the most fascinating topics in the field of digital communications. On the bright side, numerous scientists have contributed towards its body of knowledge due to its crucial role in the successful implementation of communication and storage systems. On the not-so-bright side, this knowledge has grown to an extent that it has also become the least understood and puzzling topic in the grand scheme of things. My objective in this article is to simplify the problem in a clear and intelligible manner, and also refer to some of the most widely used solutions within the explanation.
Continue reading
Fractional Delay Filters Using the Farrow Structure
In the discussion on piecewise polynomial interpolation, we emphasized on the fact that the fractional interval $\mu_m$ needs to be updated for each symbol time $mT_M$ and hence the subscript $m$ in $\mu_m$. For this reason, the interpolation process becomes a two-step procedure. Update the filter coefficients $h_p[n]$. Perform the convolution between $z(nT_S)$ and $h_p[n]$. This process can be simplified if the two steps above can be combined in such a way that $\mu_m$ update is weaved into the convolution operation. In other words, instead of a two-input hardware multiplication with two variable quantities, complexity can be reduced by restructuring
Continue reading