Monty Hall at his show Let's Make a Deal
Miscellaneous

The Reason Why the Monty Hall Problem Continues to Perplex Everyone

The Monty Hall problem is an interesting puzzle loosely based on an American TV game show Let’s Make a Deal hosted by Monty Hall. While the puzzle looked simple, it perplexed some of the brightest mathematical minds in the United States, including the great Paul Erdös who was one of the most prolific mathematicians of the 20th century. This continues to be the case today. I looked upon a number of references to find the source of confusion in the Monty Hall problem but failed. All I found was different solutions. Therefore, I built one myself with the usual from

Continue reading
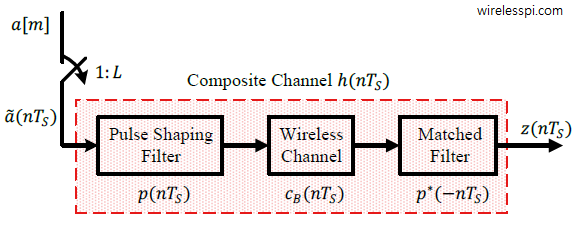
A composite channel model consisting of a pulse shaping filter, baseband channel and a matched filter
Wireless/SDR

Channel Estimation in Wireless Communication

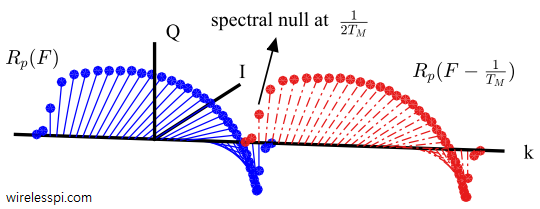
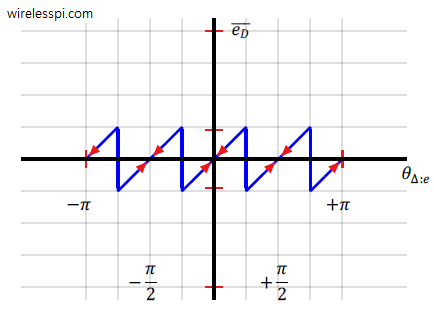
Channel estimation is a special case of the system identification problem that has a long history in the field of signal processing. The most common method to estimate a channel at the Rx is based on a training sequence (i.e., a data-aided scenario). The strategies below explain the fundamental idea of channel estimation in single-carrier systems that are still used by most advanced channel estimation techniques (aided by fancy mathematical modifications in subsequent steps). Channel estimation in OFDM systems is a topic of another article. System Parameters In this article, the modulation symbols are denoted by $a[m]$ while the channel

Continue reading
Spectrum of the Nyquist pulse and its symbol rate shifted version exhibit a spectral null at 0.5 symbol rate for a 0.5 timing offset
Wireless/SDR

Why the Performance of an Equalizer Depends on Symbol Timing Phase

This post is written on an advanced topic mainly for practitioners and researchers in the design of wireless systems. For learning about wireless communication systems from a DSP perspective (the idea behind SDRs), I recommend you have a look at my book. One of the main questions in the design of a wireless receiver is the interactions among the three main blocks, namely the timing recovery loop, the equalizer and the carrier recovery loop. Life would have been easy if input to any of these blocks was independent of the output from the others. That obviously is not the case.

Continue reading
Multiple stable lock points in the S-curve of a decision-directed loop
Wireless/SDR

Resolving Phase Ambiguity through Unique Word and Differential Encoding and Decoding

In the context of carrier synchronization, we have discussed the Costas loop and other techniques before. Today, we discuss the significance of differential encoding and decoding for phase ambiguity resolution. Keep in mind that this topic is different than differential detection. In the former case, the data bits are encoded before modulation and decoded after demodulation in a differential manner. Nevertheless, the demodulation is still coherent (i.e., it requires carrier synchronization). In the latter case, the data symbols are detected during demodulation through differential operations, thus canceling the effect of channel phase and eliminating the need for carrier synchronization. Let

Continue reading
Solution for 3 coin tosses
Miscellaneous

The Coin Toss Puzzle and the Simplest Possible Solution

Recently, I wrote an article on why the Monty Hall problem has perplexed so many brilliant minds where I showed that it was a corner case between 1 open and 1 closed door, while the intuitive but wrong answer is close to the probability curve of 1 open door. Now a coin toss puzzle has appeared on Twitter [1] that has gone viral as it goes against our common intuition of probability and random sequences (such as a series of coin tosses). The puzzle goes as follows. The Problem Flip a fair coin 100 times—it gives a sequence of heads

Continue reading