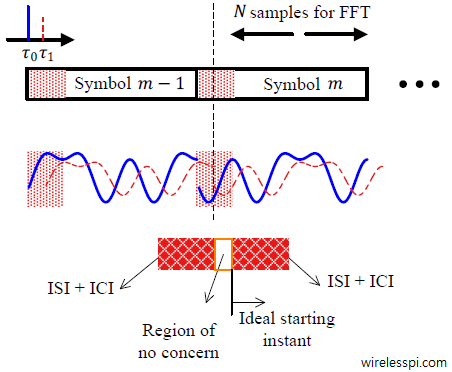
Timing synchronization is one of the most fascinating topics in the field of digital communications. The impact of symbol timing offset has been discussed in the context of single-carrier systems before. The intuition behind how an OFDM system works is also presented in a previous article. However, the problem of timing synchronization is quite different in OFDM systems as compared to single-carrier systems due to the nature of the waveform. Let us explore how a timing error impacts the demodulated waveform in such a scenario. To avoid using many indices, we skip the OFDM symbol index $m$ in the following
Continue reading