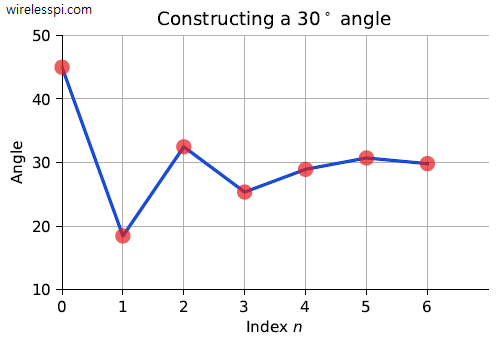
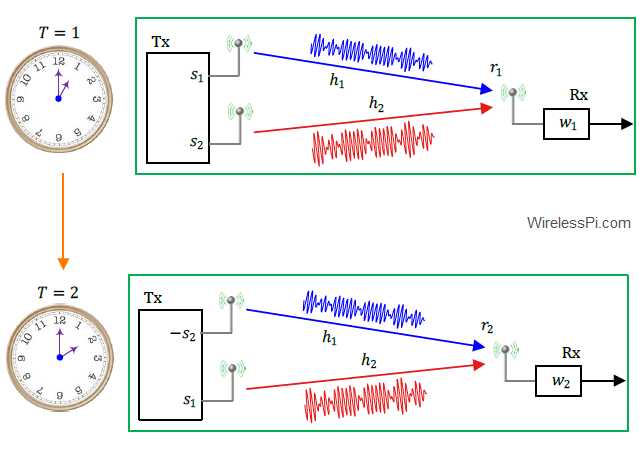
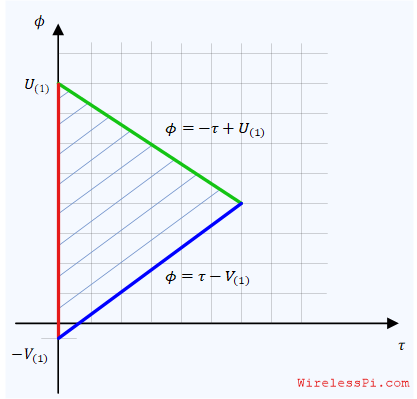
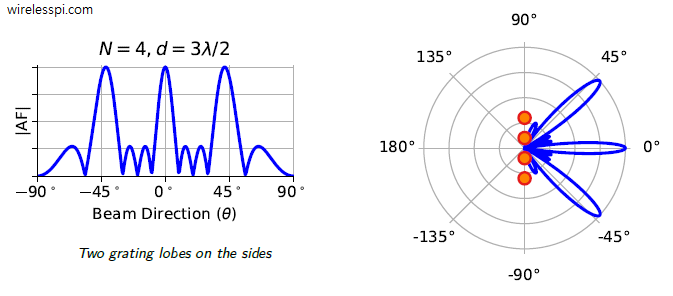
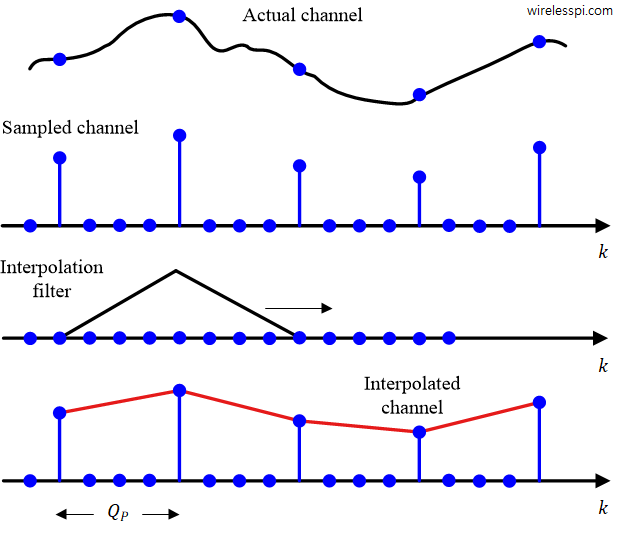
Digitial Signal Processing (DSP) plays a crucial role in algorithm implmentation for building digital and wireless communication systems. A common theme in all those algorithms is that they can be implemented with the following simple operations: addition multiplication shift In fact, these are the basic principles on which a digital signal processor is constructed. However, when it comes to implementation of real-time systems in hardware such as FPGAs, we find ways to reduce the complexity even further. Which operation (out of the above three) do you think is the most demanding in computations? It is the multiplications. Therefore, it is
Continue reading