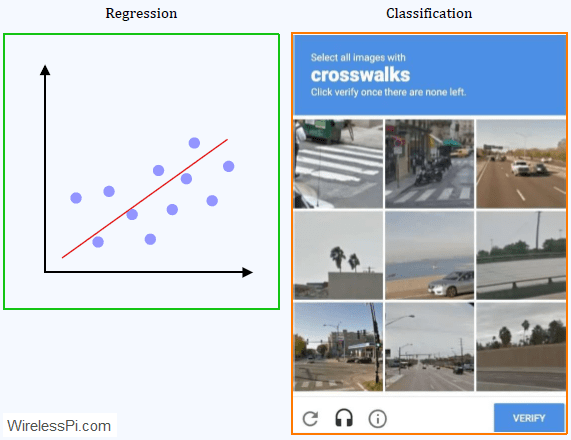
Regression and classification in supervised learning
Machine Learning

What is Supervised Learning?

In a previous article, we had a little introduction to the big picture of machine learning. More than what is it is, we focused on what it is not. Today we explore the category of supervised learning that opens the door to our understanding of advanced machine learning techniques. To see how supervised learning is proliferating in all walks of life, consider a few examples below. Insurance companies can predict the costs of storms damages for the future years due to climate change and adjust their premiums accordingly. During an interview, companies can classify the candidates with high and low

Continue reading
Interaction between populations of rabbits and foxes
DSP

Rabbits, Foxes and IQ Signals

If we pay attention, each term in a mathematical equation carries a meaning that resonates with common sense. Today I will explain where Lotka-Volterra equations come from. These equations describe the dynamics of a biological interaction in which a predator (e.g., foxes) and a prey species (e.g., rabbits) engage with each other in a continuous struggle for survival. We will see that the math expressions just line up to describe the phenomenon almost as in words. Moreover, they have a little connection to IQ signals, the fundamental concept in digital signal processing, that will also be presented in the article.

Continue reading
The effect of symbol timing offset on an OFDM symbol
Wireless/SDR

Effect of Timing Mismatch in OFDM Systems

Timing synchronization is one of the most fascinating topics in the field of digital communications. The impact of symbol timing offset has been discussed in the context of single-carrier systems before. The intuition behind how an OFDM system works is also presented in a previous article. However, the problem of timing synchronization is quite different in OFDM systems as compared to single-carrier systems due to the nature of the waveform. Let us explore how a timing error impacts the demodulated waveform in such a scenario. To avoid using many indices, we skip the OFDM symbol index $m$ in the following

Continue reading
Two tracks in an extended Kalman filter
Wireless/SDR

The Extended Kalman Filter (EKF)

I have described in detail the story of the Kalman Filter (KF) in a previous article using intuitive arguments. The Kalman filter is applicable to linear models. Today we will learn about extending the Kalman filter to non-linear scenarios through an extended Kalman filter. Numerous applications today require estimating the range, velocity, and acceleration of objects moving along a straight path. It could be an airplane within the scope of a traditional radar or an autonomous vehicle cruising down a road in an ever-connected society. And who knows, perhaps the superhumans of the next century will engage in futuristic play

Continue reading
A complex sinusoid scaled by r>1
DSP

A Visualization of Causality and Stability in z-Transform

Most of the books and resources explain the z-Transform as a mathematical concept rather than a signal processing idea. Today I will provide a simple explanation of how the z-Transform helps in determining whether a system is causal and stable. I hope that this visual approach will help my readers learn this concept in a better manner. The z-Transform For a discrete-time signal $h[n]$ (that is the impulse response of a system), the z-Transform is defined as \begin{equation}\label{equation-z-transform} H(z) = \sum _{n=-\infty}^{\infty} h[n]z^{-n} \end{equation} Then, $z$ is a complex number and hence can be written as \[ z = re^{j\omega}

Continue reading