Wireless/SDR Archives | Page 4 of 22

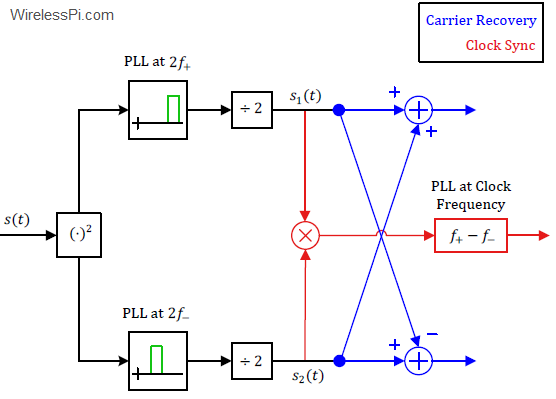
Synchronization circuit for a Minimum Shift Keying (MSK) modem

April 25, 2022 Wireless/SDR

Carrier and Clock Synchronization in MSK Signals

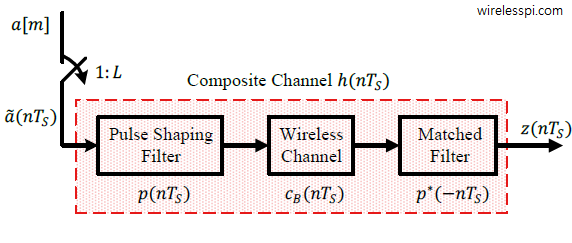
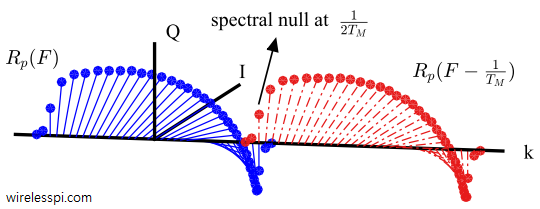
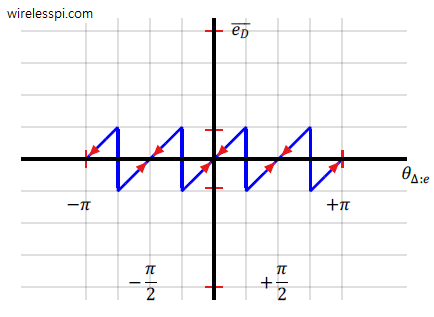
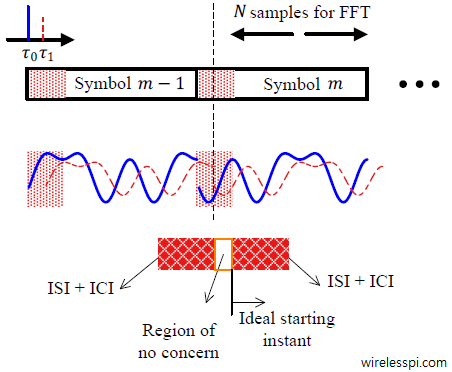
Minimum Shift Keying (MSK) is a versatile and spectrally efficient digital modulation scheme. On this website, I have previously written a tutorial on MSK in some detail. We saw how MSK is a special case of Continuous-Phase Frequency Shift Keying (CPFSK) which is a special case of Continuous-Phase Modulation (CPM). We also explored how it can also be cast as Offset Quadrature Phase Shift Keying (OQPSK). In designing a real communication system, the design of modulators and demodulators is the easy part. The main difficulty arises from acquiring synchronization with the incoming signal. Today we investigate the carrier and timing

A composite channel model consisting of a pulse shaping filter, baseband channel and a matched filter

April 18, 2022 Wireless/SDR

Channel Estimation in Wireless Communication

Channel estimation is a special case of the system identification problem that has a long history in the field of signal processing. The most common method to estimate a channel at the Rx is based on a training sequence (i.e., a data-aided scenario). The strategies below explain the fundamental idea of channel estimation in single-carrier systems that are still used by most advanced channel estimation techniques (aided by fancy mathematical modifications in subsequent steps). Channel estimation in OFDM systems is a topic of another article. System Parameters In this article, the modulation symbols are denoted by $a[m]$ while the channel

Spectrum of the Nyquist pulse and its symbol rate shifted version exhibit a spectral null at 0.5 symbol rate for a 0.5 timing offset

April 11, 2022 Wireless/SDR

Why the Performance of an Equalizer Depends on Symbol Timing Phase

This post is written on an advanced topic mainly for practitioners and researchers in the design of wireless systems. For learning about wireless communication systems from a DSP perspective (the idea behind SDRs), I recommend you have a look at my book. One of the main questions in the design of a wireless receiver is the interactions among the three main blocks, namely the timing recovery loop, the equalizer and the carrier recovery loop. Life would have been easy if input to any of these blocks was independent of the output from the others. That obviously is not the case.

Multiple stable lock points in the S-curve of a decision-directed loop

April 4, 2022 Wireless/SDR

Resolving Phase Ambiguity through Unique Word and Differential Encoding and Decoding

In the context of carrier synchronization, we have discussed the Costas loop and other techniques before. Today, we discuss the significance of differential encoding and decoding for phase ambiguity resolution. Keep in mind that this topic is different than differential detection. In the former case, the data bits are encoded before modulation and decoded after demodulation in a differential manner. Nevertheless, the demodulation is still coherent (i.e., it requires carrier synchronization). In the latter case, the data symbols are detected during demodulation through differential operations, thus canceling the effect of channel phase and eliminating the need for carrier synchronization. Let

The effect of symbol timing offset on an OFDM symbol

March 28, 2022 Wireless/SDR

Effect of Timing Mismatch in OFDM Systems

Timing synchronization is one of the most fascinating topics in the field of digital communications. The impact of symbol timing offset has been discussed in the context of single-carrier systems before. The intuition behind how an OFDM system works is also presented in a previous article. However, the problem of timing synchronization is quite different in OFDM systems as compared to single-carrier systems due to the nature of the waveform. Let us explore how a timing error impacts the demodulated waveform in such a scenario. To avoid using many indices, we skip the OFDM symbol index $m$ in the following